/Szkoła średnia/Geometria/Planimetria/Trójkąt

Zadanie nr 9599171

Dodaj do ulubionych
Dodaj do rozwiązanych

Oblicz długości boków trójkąta prostokątnego, którego obwód wynosi 40, a pole 60.

Rozwiązanie

Jeżeli oznaczymy 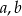a ,b – przyprostokątne, a c – przeciwprostokątna, to mamy układ

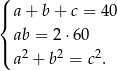
( |{ a+ b+ c = 40 ab = 2 ⋅60 |( 2 2 2 a + b = c .

Pierwsza równość to warunek z obwodem, druga z polem, a trzecia to twierdzenie Pitagorasa. Przekształcimy teraz pierwszą równość, korzystając z dwóch pozostałych.

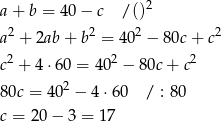
a+ b = 40 − c / ()2 2 2 2 2 a + 2ab+ b = 40 − 80c + c 2 2 2 c + 4⋅60 = 40 − 80c + c 80c = 40 2 − 4 ⋅60 / : 80 c = 20 − 3 = 1 7

Pierwsze dwa równania układu przyjmują więc postać

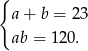
{ a+ b = 23 ab = 120.

Można ten układ łatwo rozwiązać korzystając ze wzorów Viète’a – liczby 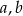a,b są pierwiastkami równania

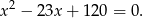
x2 − 23x + 1 20 = 0.

Jeżeli jednak nie chcemy korzystać ze wzorów Viète’a, to podstawiamy 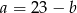a = 23− b z pierwszego równania do drugiego.

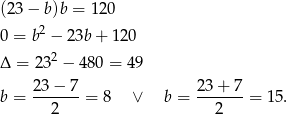
(23 − b)b = 120 2 0 = b − 2 3b+ 120 Δ = 232 − 480 = 49 b = 23-−-7-= 8 ∨ b = 23-+-7-= 15. 2 2

Mamy wtedy odpowiednio 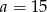a = 1 5 i a = 8 .  
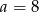Odpowiedź: 8,15,17

Wersja PDF