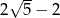/Szkoła średnia/Geometria/Planimetria/Trójkąt

Zadanie nr 9610018

Dodaj do ulubionych
Dodaj do rozwiązanych

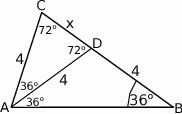
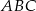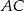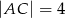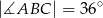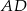W trójkącie równoramiennym ABC o podstawie AC dane są: |AC | = 4 oraz |∡ABC | = 36∘ . Odcinek AD jest odcinkiem dwusiecznej kąta 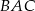BAC (zobacz rysunek).

PIC

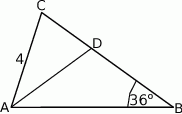
Oblicz długość odcinka 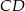CD .

Rozwiązanie

Trójkąt 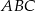ABC jest równoramienny, więc

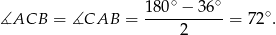
180∘ − 36 ∘ ∡ACB = ∡CAB = -----------= 72∘. 2

Odcinek 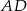AD jest zawarty w dwusiecznej kąta 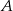A , więc

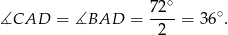
72∘ ∘ ∡CAD = ∡BAD = ----= 36 . 2

Stąd

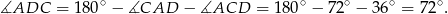
∡ADC = 180∘ − ∡CAD − ∡ACD = 180∘ − 72∘ − 36 ∘ = 72∘.

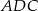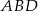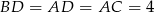W szczególności trójkąty ADC i ABD są równoramienne i BD = AD = AC = 4 .

PIC

Oznaczmy 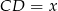CD = x . Z podobieństwa trójkątów ADC i BAC mamy

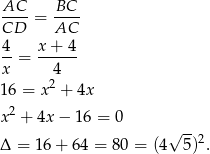
AC--= BC-- CD AC 4- x+--4- x = 4 2 16 = x + 4x x2 + 4x − 16 = 0 √ --2 Δ = 1 6+ 64 = 80 = (4 5) .

Dodatni pierwiastek tego równania to 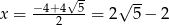√ - √ -- x = −-4+24--5= 2 5 − 2  
Odpowiedź: 2√ 5-− 2

Wersja PDF