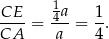Zadanie nr 9700205
Trójkąt 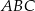 jest równoboczny. Punkt
jest równoboczny. Punkt 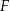 leży na wysokości
leży na wysokości 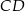 tego trójkąta oraz
tego trójkąta oraz 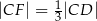 . Punkt
. Punkt 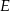 leży na boku
leży na boku 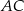 i odcinek
i odcinek 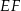 jest prostopadły do
jest prostopadły do 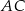 (zobacz rysunek).
(zobacz rysunek).
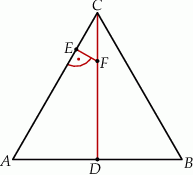
Wykaż, że 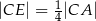 .
.
Rozwiązanie
Sposób I
Trójkąt 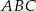 jest równoboczny, więc
jest równoboczny, więc
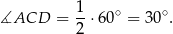
Patrzymy teraz na trójkąty prostokątne 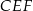 i
i 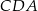 .
.
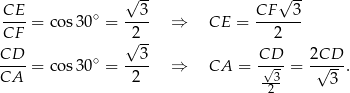
Stąd
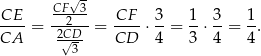
Sposób II
Oznaczmy przez 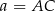 długość boku trójkąta równobocznego
długość boku trójkąta równobocznego 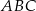 . Mamy zatem
. Mamy zatem
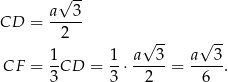
Długość odcinka 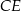 możemy obliczyć z podobieństwa trójkątów
możemy obliczyć z podobieństwa trójkątów 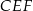 i
i 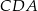 , lub też wprost z trójkąta prostokątnego
, lub też wprost z trójkąta prostokątnego 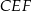 :
:
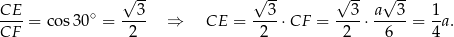
Stąd