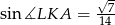/Szkoła średnia/Geometria/Planimetria/Trójkąt

Zadanie nr 9765920

Dodaj do ulubionych
Dodaj do rozwiązanych

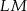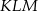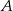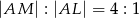Na boku LM trójkąta równobocznego KLM obrano taki punkt A , że |AM | : |AL | = 4 : 1 .

  • Oblicz stosunek pól trójkątów 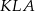KLA i KAM .
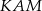  • Oblicz stosunek promieni okręgów opisanych na tych trójkątach.
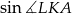  • Wyznacz sin∡LKA .

Rozwiązanie

Zaczynamy od rysunku.

PIC

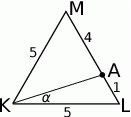
  • Trójkąty te mają wspólną wysokość opuszczoną z wierzchołka 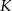K , zatem stosunek pól jest taki sam jak stosunek podstaw, czyli 1:4.  
    Odpowiedź: 1:4
  •  

    Sposób I

    Na mocy twierdzenia sinusów mamy

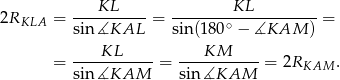
    KL KL 2RKLA = ---------- = -------∘------------= sin ∡KAL sin (180 − ∡KAM ) ----KL----- ---KM------ = sin ∡KAM = sin ∡KAM = 2RKAM .

    Promienie te są więc równe.

    Sposób II

    Na mocy twierdzenia sinusów

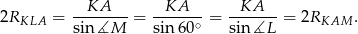
    2R = --KA----= --KA--- = --KA--- = 2R . KLA sin∡M sin6 0∘ sin ∡L KAM

    Promienie te są więc równe.  
    Odpowiedź: 1

  • Szukany sinus obliczymy z twierdzenia sinusów w trójkącie 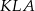KLA , najpierw jednak wyliczymy (z twierdzenia cosinusów) długość odcinka 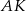AK . Aby to zrobić przyjmijmy, że bok trójkąta 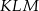KLM ma długość 5 (5, a nie 1, żeby nie mieć ułamków).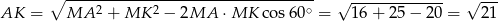
    ∘ ----2------2--------------------∘- √ ------------- √ --- AK = MA + MK − 2MA ⋅MK co s60 = 16+ 25− 20 = 21

    Zatem na mocy twierdzenia sinusów w trójkącie 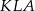KLA mamy

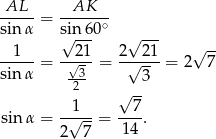
    -AL--= --AK--- sinα s√in-60∘ √ --- 1 21 2 2 1 √ -- -----= -√---= -√---- = 2 7 sinα -23 3 √ -- sinα = -√1--= --7-. 2 7 14

     
    Odpowiedź: √7- sin ∡LKA = 14

Wersja PDF