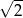Zadanie nr 9784365
W trójkącie prostokątnym 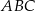 , w którym
, w którym 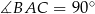 i
i 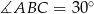 , wybrano na przyprostokątnej
, wybrano na przyprostokątnej 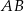 punkt
punkt 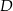 tak, że
tak, że 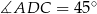 . Oblicz stosunek długości odcinków
. Oblicz stosunek długości odcinków 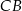 i
i 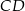 .
.
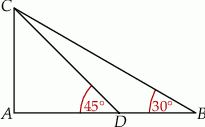
Rozwiązanie
Sposób I
Z definicji funkcji trygonometrycznych mamy
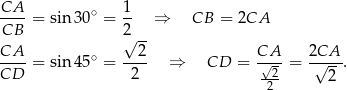
Mamy zatem
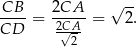
Sposób II
Korzystamy z twierdzenia sinusów w trójkącie  .
.
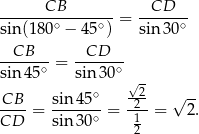
Odpowiedź: