/Szkoła średnia/Geometria/Planimetria/Trójkąt

Zadanie nr 9786220

Dodaj do ulubionych
Dodaj do rozwiązanych

Wykaż, że jeżeli długości boków 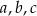a,b,c trójkąta prostokątnego są liczbami całkowitymi, to liczba 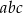abc jest parzysta.

Rozwiązanie

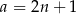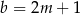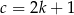Niech c będzie przeciwprostokątną danego trójkąta oraz załóżmy, że wszystkie trzy podane długości boków są liczbami nieparzystymi, tzn. a = 2n+ 1 , b = 2m + 1 , c = 2k + 1 dla pewnych liczb całkowitych 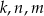k,n,m . Na mocy twierdzenia Pitagorasa mamy

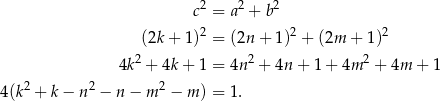
c2 = a2 + b2 2 2 2 (2k + 1) = (2n + 1 ) + (2m + 1) 4k2 + 4k + 1 = 4n 2 + 4n + 1+ 4m 2 + 4m + 1 4(k2 + k− n 2 − n− m2 − m ) = 1.

To jednak nie jest możliwe, bo lewa strona dzieli się przez 4, a prawa nie. W takim razie nie mogą wszystkie trzy liczby 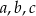a,b,c być liczbami nieparzystymi, więc jedna z nich jest parzysta. To oznacza, że iloczyn 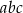abc jest liczbą parzystą.

Wersja PDF