Zadanie nr 9854569
Dwa boki trójkąta wpisanego w okrąg o promieniu 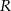 są odpowiednio równe
są odpowiednio równe 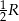 i
i 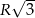 . Oblicz długość trzeciego boku.
. Oblicz długość trzeciego boku.
Rozwiązanie
Jak zwykle zaczynamy od rysunku.
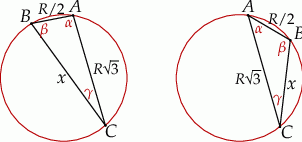
Robiąc go można zauważyć, że możliwe są dwie konfiguracje: gdy narysujemy już cięciwę długości 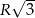 to cięciwę długości
to cięciwę długości 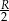 możemy narysować na dwa sposoby – po dwóch stronach pierwszej z cięciw. Przypadki te różnią się tym, że w jednym z nich zaznaczony kąt
możemy narysować na dwa sposoby – po dwóch stronach pierwszej z cięciw. Przypadki te różnią się tym, że w jednym z nich zaznaczony kąt  jest ostry, a w drugim rozwarty. Jeżeli byśmy nie zauważyli drugiego przypadku, to nic by się nie stało, bo i tak wyjdzie on nam w rachunkach.
jest ostry, a w drugim rozwarty. Jeżeli byśmy nie zauważyli drugiego przypadku, to nic by się nie stało, bo i tak wyjdzie on nam w rachunkach.
Sposób I
Długość trzeciego boku trójkąta obliczymy z twierdzenia sinusów, ale zanim to zrobimy, obliczmy funkcje trygonometryczne pozostałych dwóch kątów trójkąta. Stosujemy twierdzenie sinusów. Stosujemy twierdzenie sinusów.
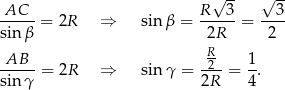
Z jedynki trygonometrycznej obliczymy teraz cosinusy tych kątów. Zanim to jednak zrobimy, zauważmy, że kąt 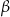 leży na przeciwko dłuższego boku niż kąt
leży na przeciwko dłuższego boku niż kąt 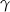 , więc kąt
, więc kąt 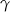 na pewno jest ostry, a kąt
na pewno jest ostry, a kąt 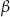 może być ostry lub rozwarty. Mamy zatem
może być ostry lub rozwarty. Mamy zatem
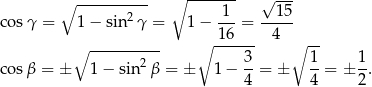
Wybór znaku przy 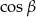 geometrycznie odpowiada dwóm możliwym konfiguracjom, które zauważyliśmy na początku rozwiązania. Możemy teraz obliczyć
geometrycznie odpowiada dwóm możliwym konfiguracjom, które zauważyliśmy na początku rozwiązania. Możemy teraz obliczyć 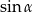 – korzystamy ze wzoru na sinus sumy.
– korzystamy ze wzoru na sinus sumy.
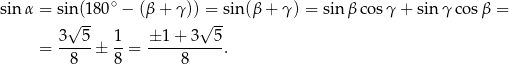
Stosujemy teraz twierdzenie sinusów.
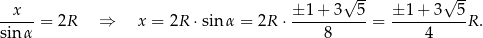
Sposób II
Pomysł jest taki, żeby obliczyć szukaną długość  trzeciego boku z twierdzenia cosinusów. Aby to zrobić, potrzebujemy znać
trzeciego boku z twierdzenia cosinusów. Aby to zrobić, potrzebujemy znać 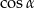 . Dokładnie tak samo jak w poprzednim sposobie obliczamy wartości funkcji trygonometrycznych kątów
. Dokładnie tak samo jak w poprzednim sposobie obliczamy wartości funkcji trygonometrycznych kątów 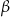 i
i 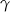 . To pozwala obliczyć
. To pozwala obliczyć 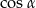 – korzystamy ze wzoru na cosinus sumy.
– korzystamy ze wzoru na cosinus sumy.
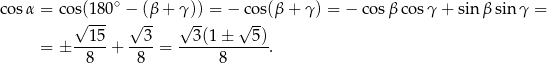
Stosujemy teraz twierdzenie cosinusów
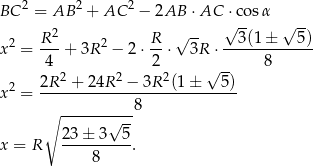
Sposób III
Jak poprzednio chcemy obliczyć 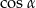 . Stosujemy twierdzenie sinusów (bo znamy promień okręgu opisanego).
. Stosujemy twierdzenie sinusów (bo znamy promień okręgu opisanego).
Liczymy
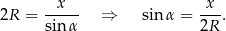
Teraz obliczymy 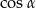 z jedynki trygonometrycznej – będziemy mieli problem z wyborem znaku, ale to dokładnie odpowiada dwóm możliwym konfiguracjom.
z jedynki trygonometrycznej – będziemy mieli problem z wyborem znaku, ale to dokładnie odpowiada dwóm możliwym konfiguracjom.
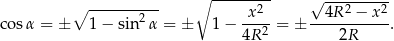
Stosujemy teraz twierdzenie cosinusów
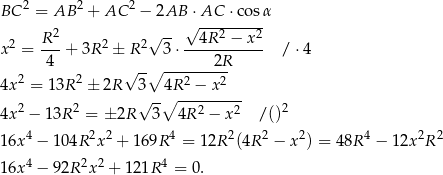
Podstawiamy 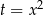 i dzielimy równanie stronami przez 4.
i dzielimy równanie stronami przez 4.
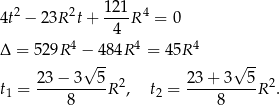
Zatem
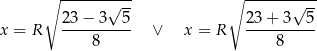
Sposób IV
Tym razem, pomimo podobnego schematu, najpierw obliczymy 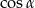 w zależności od
w zależności od 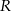 , a dopiero potem
, a dopiero potem  . Podobnie jak poprzednio piszemy twierdzenie cosinusów
. Podobnie jak poprzednio piszemy twierdzenie cosinusów
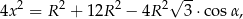
ale tym razem podstawiamy za 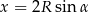 .
.
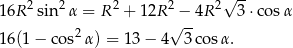
Podstawiamy 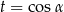 .
.
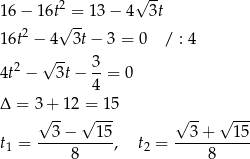
Wracając do twierdzenia cosinusów otrzymujemy
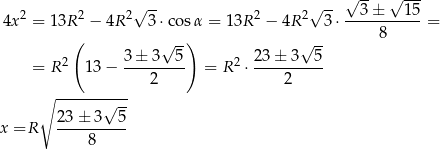
Sposób V
Tym razem również będziemy łączyć ze sobą twierdzenia sinusów i cosinusów, ale skoncentrujemy się na kącie 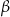 .
.
Jak popatrzymy na II sposób rozwiązania, to tam najważniejszym problem było to, że w wyrażeniu na 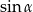 występował
występował  . Jeżeli zmienimy kąt to pozbędziemy się tego problemu (kosztem skomplikowania twierdzenia cosinusów). Tym razem mamy
. Jeżeli zmienimy kąt to pozbędziemy się tego problemu (kosztem skomplikowania twierdzenia cosinusów). Tym razem mamy
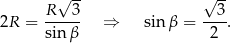
Tu jest delikatny moment, bo z powyższej równości nie wynika, że 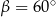 , może być też
, może być też 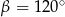 – to są dokładnie te dwa przypadki z początku rozwiązania. Tak czy inaczej
– to są dokładnie te dwa przypadki z początku rozwiązania. Tak czy inaczej
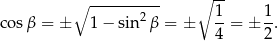
Piszemy teraz twierdzenie cosinusów.
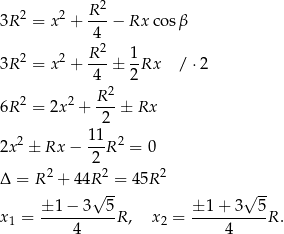
Ponieważ obie wartości 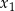 są ujemne pozostaje nam
są ujemne pozostaje nam
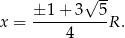
Odpowiedź: