/Szkoła średnia/Geometria/Planimetria/Trójkąt

Zadanie nr 9981316

Dodaj do ulubionych
Dodaj do rozwiązanych

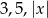Wyznacz wszystkie wartości x , dla których liczby 3 ,5,|x | mogą być długościami boków trójkąta.

Rozwiązanie

Trójkąt o bokach 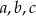a ,b,c istnieje o ile

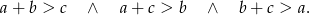
a+ b > c ∧ a + c > b ∧ b + c > a .

Tak naprawdę, to wystarczy aby była spełniona tylko jedna z tych nierówności: ta w której najdłuższy bok jest po prawej stronie. Oczywiście nie zawsze wiemy, który bok jest najdłuższy (np. w zadaniach z parametrem).

Muszą być spełnione dwa warunki (bo bok długości 3 nie jest najdłuższym bokiem).

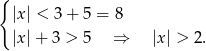
{ |x| < 3 + 5 = 8 |x| + 3 > 5 ⇒ |x | > 2 .

Mamy zatem

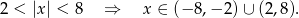
2 < |x| < 8 ⇒ x ∈ (− 8,− 2) ∪ (2,8).

 
Odpowiedź: x ∈ (− 8,− 2) ∪ (2,8)

Wersja PDF