/Gimnazjum/Egzamin gimnazjalny/Egzamin 2013
Próbny Egzamin Gimnazjalny
z Matematyki Zestaw przygotowany przez serwis www.zadania.info 6 kwietnia 2013 Czas pracy: 90 minut
Dokończ zdanie tak, aby otrzymać zdanie prawdziwe.
Wyrażenie 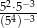 ma wartość
ma wartość
A) 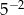 B)
B) 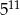 C)
C) 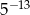 D)
D) 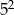
Dokończ zdanie tak, aby otrzymać zdanie prawdziwe.
Na osi liczbowej narysowano odcinek, którego końcami są największa i najmniejsza spośród liczb 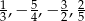 . Długość tego odcinka jest równa
. Długość tego odcinka jest równa
A) 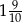 B)
B) 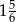 C)
C) 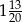 D)
D) 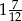
Informacja do zadań 3 i 4
Parkieciarz w ciągu 6 dni ułożył parkiet liczący 4800 klepek.
| Dzień | Liczba ułożonych klepek | Czas pracy |
| 1. | 700 | 5 h 40 min |
| 2. | 900 | 6 h |
| 3. | 600 | 5 h 20 min |
| 4. | 1000 | 6 h 30 min |
| 5. | 1100 | 6 h 10 min |
| 6. | 500 | 4 h 20 min |
Na podstawie informacji zawartych w powyższej tabeli wybierz zdanie fałszywe.
A) Parkieciarz średnio układał 800 klepek dziennie.
B) Trzeciego dnia parkieciarz ułożył 12,5% parkietu.
C) W ciągu dwóch ostatnich dni parkieciarz ułożył 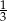 całego parkietu.
całego parkietu.
D) Łączny czas pracy parkieciarza w ciągu trzech pierwszych dni był krótszy, niż łączny czas pracy w ciągu trzech następnych dni.
Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
| W ciągu dwóch dni pracy tempo układania klepek było mniejsze niż 2 klepki na minutę. | P | F |
| Najwolniej parkieciarz układał klepki 6 dnia. | P | F |
Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
| Liczba 3480 jest liczbą podzielną przez 45. | P | F |
| Liczba 3480 jest wielokrotnością 16. | P | F |
Ula i Kajtek mają razem 22 lata. Pięć lat temu Ula była 3 razy starsza od Kajtka.
Ile lat temu Ula była dwa razy starsza od Kajtka?
Wybierz odpowiedź spośród podanych.
A) 1 B) 2 C) 3 D) 4
Na rysunku przedstawiono wykres pewnej funkcji.
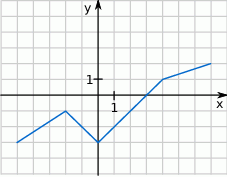
Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
Funkcja przyjmuje wartość 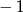 dla argumentu dla argumentu 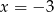 . . | P | F |
Dla wszystkich argumentów 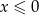 funkcja przyjmuje wartości ujemne. funkcja przyjmuje wartości ujemne. | P | F |
Informacja do zadań 8 i 9
W stadninie koni pani Lucyny znajduje się 120 koni w czterech różnych umaszczeniach. Na diagramie przedstawiono w procentach udział poszczególnych umaszczeń, ale nie narysowano słupka z umaszczeniem karym.
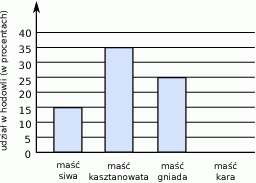
Ile jest koni gniadych w hodowli pani Lucyny? Wybierz odpowiedź spośród podanych.
A) 15 B) 20 C) 25 D) 30
Jaki procent hodowli pani Lucyny stanowią konie kare? Wybierz odpowiedź spośród podanych.
A) 15% B) 20% C) 25% D) 30%
Informacja do zadań 10 i 11
Z pudełka, w którym znajdują się 3 piłki niebieskie, 2 piłki czerwone i 5 piłek żółtych losujemy dwie piłki i odkładamy je na bok. Następnie losujemy z tego pudełka jeszcze jedną piłkę.
Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
| Jeżeli prawdopodobieństwo wylosowania piłki czerwonej w drugim losowaniu jest równe 0, to w pierwszym losowaniu wyciągnięto dwie piłki czerwone. | P | F |
Jeżeli prawdopodobieństwo wylosowania piłki czerwonej w drugim losowaniu jest równe 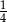 , to w pierwszym losowaniu nie wyciągnięto żadnej piłki czerwonej. , to w pierwszym losowaniu nie wyciągnięto żadnej piłki czerwonej. | P | F |
Dokończ zdanie tak, aby otrzymać zdanie prawdziwe.
Jeżeli w pierwszym losowaniu nie wylosowano piłki niebieskiej to prawdopodobieństwo wylosowania piłki niebieskiej w drugim losowaniu
A) może być równe prawdopodobieństwu wylosowania piłki czerwonej.
B) może być równe prawdopodobieństwu wylosowania piłki żółtej.
C) jest równe 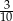
D) jest równe 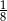
Do udziału w podchodach zgłosiło się 54 chłopców i 24 dziewczynki. Uczestników postanowiono podzielić na zespoły w ten sposób, aby we wszystkich zespołach była ta sama liczba dziewcząt i ta sama liczba chłopców.
Ile maksymalnie zespołów utworzono? Wybierz odpowiedź spośród podanych.
A) 9 B) 2 C) 3 D) 6
Jacek i Ewa mieli w maju odpowiednio 1200 i 2000 złotych oszczędności. W czerwcu oszczędności Jacka wzrosły o 25%, ale w sumie mieli z Ewą nadal tyle samo oszczędności co w maju.
O ile procent zmalały w czerwcu oszczędności Ewy? Wybierz odpowiedź spośród podanych.
A) 15% B) 17,6% C) 25% D) 30%
Od kartonika w kształcie trójkąta równobocznego odcięto naroża, tak jak pokazano na rysunku i otrzymano sześciokąt foremny o bokach długości 3.
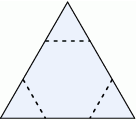
Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
| Kartonik był trójkątem o obwodzie 27. | P | F |
| Suma pól odciętych naroży jest dwa razy mniejsza od pola sześciokąta. | P | F |
Na siatce kwadratowej narysowano trójkąt. Bok kwadratu siatki jest równy 1.
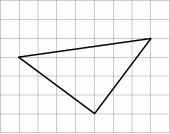
Dokończ zdanie, wybierając odpowiedź spośród podanych.
Obwód narysowanego trójkąta jest równy
A) 76 B) 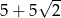 C)
C) 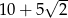 D) 75
D) 75
Nadajnik telekomunikacyjny znajduje się w punkcie 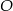 (niezaznaczonym na rysunku), który jest jednakowo oddalony od trzech dróg łączących miasta
(niezaznaczonym na rysunku), który jest jednakowo oddalony od trzech dróg łączących miasta 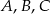 .
.

Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
Punkt 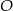 jest punktem przecięcia dwusiecznych kątów trójkąta jest punktem przecięcia dwusiecznych kątów trójkąta 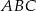 . . | P | F |
Punkt 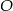 jest środkiem okręgu opisanego na trójkącie jest środkiem okręgu opisanego na trójkącie 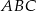 . . | P | F |
Dokończ zdanie, wybierając odpowiedź spośród podanych.
Pole trójkąta wynosi 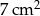 . Pole trójkąta do niego podobnego jest równe
. Pole trójkąta do niego podobnego jest równe 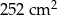 . Skala podobieństwa trójkąta mniejszego do większego jest równa
. Skala podobieństwa trójkąta mniejszego do większego jest równa
A) 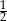 B)
B) 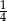 C)
C)  D)
D) 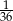
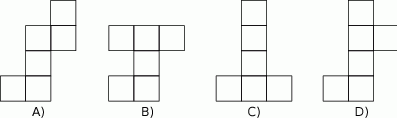
Który z poniższych rysunków nie może być siatką sześcianu? Wybierz odpowiedź spośród podanych.
Zbiornik retencyjny ma kształt walca o wysokości 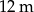 . Do zbiornika wlano
. Do zbiornika wlano 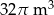 wody, która wypełniła go do
wody, która wypełniła go do  wysokości.
wysokości.
Jaka jest średnica podstawy tego zbiornika? Wybierz odpowiedź spośród podanych.
A) 0,5 m B) 1 m C) 2 m D) 4 m
Wykonano następującą konstrukcję.
1. Narysowano trapez równoramienny 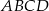 , w którym
, w którym 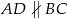 .
.
2. Wykreślono symetralne odcinków 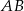 i
i 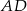 i ich punkt przecięcia oznaczono literą
i ich punkt przecięcia oznaczono literą 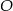 .
.
3. Narysowano okrąg o środku w punkcie 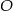 i promieniu
i promieniu 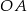 .
.
Dokończ poniższe zdanie, wybierając odpowiedź spośród podanych.
Skonstruowany w opisany powyżej sposób okrąg
A) przechodzi przez wszystkie wierzchołki tego trapezu.
B) jest styczny do wszystkich boków tego trapezu.
C) jest styczny do podstaw tego trapezu.
D) przechodzi przez środki ramion trapezu.
Troje przyjaciół: Adam, Wojtek i Karol postanowiło kupić losy na loterii, w której jeden los kosztował 4 zł. Adam kupił 12 losów, Wojtek kupił 9 losów, a Karol kupił 3 losy. Po sprawdzeniu wszystkich losów okazało się, że chłopcy wygrali w sumie 168 zł. Wygraną kwotę postanowili podzielić następująco: każdy z chłopców z wygranej kwoty zabrał tyle pieniędzy, ile wydał na losy, a pozostałą kwotę chłopcy podzieli między siebie, proporcjonalnie do liczby kupionych losów. Ile pieniędzy z wygranych 168 zł otrzymał każdy z chłopców? Zapisz obliczenia.
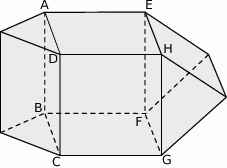
Na rysunku przedstawiono bryłę, której każda ściana jest albo kwadratem, albo trójkątem równobocznym. Kwadratami są też czworokąty 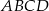 i
i  . Każda krawędź ma długość 4. Jaką objętość ma ta bryła? Zapisz obliczenia.
. Każda krawędź ma długość 4. Jaką objętość ma ta bryła? Zapisz obliczenia.
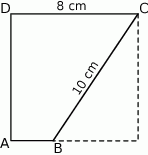
Z kwadratu o boku długości 8 cm wycięto trójkąt prostokątny o przeciwprostokątnej długości 10 cm w sposób pokazany na rysunku. Oblicz pole otrzymanego czworokąta 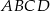 . Zapisz obliczenia.
. Zapisz obliczenia.