/Gimnazjum/Egzamin gimnazjalny/Egzamin 2013/Próbne testy
Próbny Egzamin Gimnazjalny
z Matematyki Zestaw przygotowany przez serwis www.zadania.info 20 kwietnia 2013 Czas pracy: 90 minut
Do papierowej torebki, w której znajdowały się tylko czerwone kulki dorzucono 12 żółtych kulek i okazało się, że kulki żółte stanowią 20% wszystkich kulek w torebce.
Ile czerwonych kulek było początkowo w torebce? Wybierz odpowiedź spośród podanych.
A) 24 B) 32 C) 48 D) 60
Do zestawu liczb: 2, 5, 8, 11, 12 dopisano dwie liczby. Mediana powiększonego zestawu wynosi 7.
Które z poniższych liczb dopisano? Wybierz odpowiedź spośród podanych.
A) 6 i 12 B) 7 i 12 C) 1 i 7 D) 1 i 6
Dokończ zdanie tak, aby otrzymać zdanie prawdziwe.
Odległość dwóch liczb na osi liczbowej jest równa 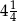 . Mniejsza z tych liczb jest równa
. Mniejsza z tych liczb jest równa 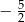 . Większa z tych liczb jest równa
. Większa z tych liczb jest równa
A) 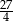 B)
B)  C)
C) 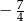 D)
D) 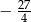
Danych jest pięć liczb
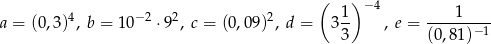
Która równość jest fałszywa? Wybierz odpowiedź spośród podanych.
A) 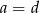 B)
B) 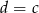 C)
C) 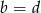 D)
D) 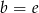 E)
E) 
Dokończ zdanie. Wybierz odpowiedź spośród podanych. Przedstawiona na wykresie funkcja przyjmuje wartości dodatnie jeżeli
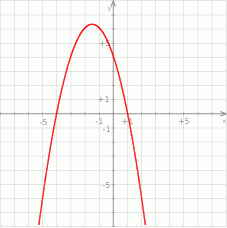
A) 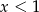 B)
B) 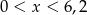 C)
C) 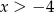 D)
D) 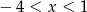
Informacja do zadań 6 i 7
W trakcie dziesięciu godzin otwarcia sklepu, właściciel prowadził obserwację liczby klientów, którzy odwiedzili ten sklep. Wynik tej obserwacji przedstawiono na wykresie.
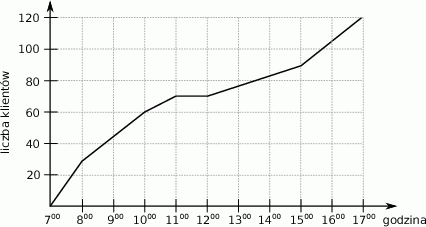
Na podstawie wykresu wybierz zdanie fałszywe.
A) Od 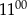 do
do 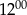 do sklepu nie przyszedł żaden klient.
do sklepu nie przyszedł żaden klient.
B) W godzinach od 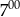 do
do 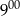 sklep odwiedziło mniej klientów niż od
sklep odwiedziło mniej klientów niż od 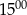 do
do 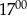 .
.
C) W ciągu pierwszej godziny sklep odwiedziło więcej klientów niż w ciągu drugiej godziny.
D) W ciągu trzech pierwszych godzin pracy sklep odwiedziło tylu samo klientów, co w ciągu pozostałych godzin pracy.
Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
| Średnio w ciągu jednej godziny obserwacji sklep odwiedzało 12 klientów. | P | F |
| Gdyby właściciel zakończył obserwację po 8 godzinach to średnia liczba klientów w ciągu godziny byłaby wyższa. | P | F |
Pan Tadeusz postanowił pomalować ściany w swoim mieszkaniu. Łączna powierzchnia ścian, które postanowił pomalować jest równa 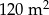 . Pod uwagę wziął dwa rodzaje farb.
. Pod uwagę wziął dwa rodzaje farb.
| Rodzaj farby | Wydajność | Cena |
| Fabra lateksowa | 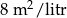 | 5 zł za 1 litr |
| Farba akrylowa | 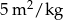 | 3 zł za 1 kg |
Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
Koszt pomalowania 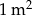 ściany jest niższy w przypadku farby akrylowej, niż w przypadku farby lateksowej. ściany jest niższy w przypadku farby akrylowej, niż w przypadku farby lateksowej. | P | F |
| Kupując tańszą farbę, pan Tadeusz zaoszczędzi 5 zł. | P | F |
Dokończ zdanie, wybierając odpowiedź spośród podanych.
Równość 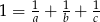 będzie prawdziwa, jeśli w miejsce
będzie prawdziwa, jeśli w miejsce 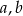 i
i  zostaną wpisane liczby
zostaną wpisane liczby
A) 2, 3, 4 B) 3, 4, 6 C) 2, 3, 6 D) 3, 4, 8
Informacja do zadań 10 – 12
Zaczynając od punktu 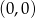 budujemy łamaną, której część składającą się z 6 odcinków przedstawiono na rysunku. Kolejne odcinki łamanej numerujemy kolejnymi liczbami naturalnymi. Drugi odcinek łamanej ma długość 2.
budujemy łamaną, której część składającą się z 6 odcinków przedstawiono na rysunku. Kolejne odcinki łamanej numerujemy kolejnymi liczbami naturalnymi. Drugi odcinek łamanej ma długość 2.
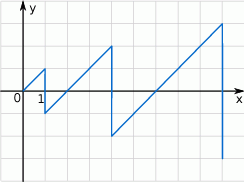
Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
Jeżeli  jest liczbą nieparzystą, to odcinek o numerze jest liczbą nieparzystą, to odcinek o numerze  jest równoległy doodcinka o numerze 1. jest równoległy doodcinka o numerze 1. | P | F |
Jeżeli  jest liczbą parzystą, to długość odcinka o numerze jest liczbą parzystą, to długość odcinka o numerze  jest równa jest równa 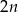 . . | P | F |
Dokończ zdanie, wybierając odpowiedź spośród podanych. Wierzchołek łamanej, którego druga współrzędna jest równa 2013 jest punktem wspólnym odcinków łamanej o numerach
A) 2012 i 2013 B) 2013 i 2014 C) 4025 i 4026 D) 4026 i 4027
Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
Długość odcinka o numerze 5 jest równa 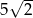 . . | P | F |
Jeżeli  jest liczbą parzystą, to długość odcinka o numerze jest liczbą parzystą, to długość odcinka o numerze 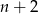 jest o 2 większa od długości odcinka o numerze jest o 2 większa od długości odcinka o numerze  . . | P | F |
Maszyna pakująca pakuje przyprawę w 200 gramowe saszetki z prędkością 2,4 tony przyprawy na godzinę.
Ile saszetek maszyna zapakuje w ciągu 8 minut? Wybierz odpowiedź spośród podanych.
A) 1600 saszetek B) 200 saszetek C) 2400 saszetek D) 1200 saszetek
W tabeli przedstawiono liczbę i rodzaj kul umieszczonych w czterech pudełkach. Z każdego pudełka losujemy jedną kulę.
| Liczba kul zielonych | Liczba kul niebieskich | Liczba kul czerwonych | |
| Pudełko nr 1 | 4 | 8 | 5 |
| Pudełko nr 2 | 7 | 16 | 9 |
| Pudełko nr 3 | 2 | 7 | 3 |
| Pudełko nr 4 | 7 | 12 | 5 |
Dokończ zdanie, wybierając odpowiedź spośród podanych.
Prawdopodobieństwo wylosowania niebieskiej kuli jest największe, gdy kulę losujemy z pudełka nr
A) 1 B) 2 C) 3 D) 4
Dokończ zdanie, wybierając odpowiedź spośród podanych.
W trapezie równoramiennym o obwodzie 21 cm suma długości ramienia i krótszej podstawy jest równa 8 cm. Różnica długości podstaw tego trapezu jest równa
A) 10 cm B) 13 cm C) 5 cm D) 2,5 cm
Pola dwóch trójkątów równobocznych są równe odpowiednio 7 i 63.
Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
| Obwód drugiego trójkąta jest 9 razy większy od obwodu pierwszego trójkąta. | P | F |
Pierwszy trójkąt jest podobny do drugiego w skali 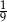 | P | F |
Na siatce kwadratowej narysowano równoległobok. Bok kwadratu siatki jest równy 1.
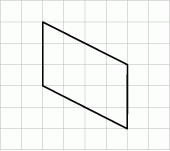
Dokończ zdanie, wybierając odpowiedź spośród podanych.
Pole narysowanego równoległoboku jest równe
A) 3 B) 6 C) 12 D) 18
Narysowana poniżej figura składa się z kwadratu, dwóch ćwiartek, oraz połówki koła.
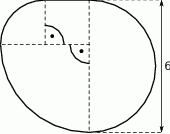
Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
Pole narysowanej figury jest równe 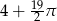 | P | F |
Obwód narysowanej figury jest równy 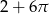 | P | F |
Na rysunku przedstawiono walec, stożek i kulę oraz niektóre ich wymiary.
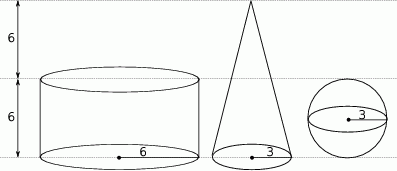
Na podstawie informacji przedstawionych na rysunku wybierz zdanie fałszywe.
A) Objętość kuli jest równa objętości stożka.
B) Objętość walca jest 3 razy większa od objętości stożka.
C) Objętość walca jest 6 razy większa od objętości kuli.
D) Suma objętości stożka i kuli jest mniejsza od objętości walca.
Do pomalowania wszystkich ścian graniastosłupa czworokątnego zużyto 30 mililitrów farby o wydajności 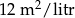 .
.
Dokończ zdanie, wybierając odpowiedź spośród podanych. Pole powierzchni tego graniastosłupa jest równe
A) 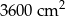 B)
B) 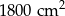 C)
C) 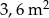 D)
D) 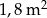
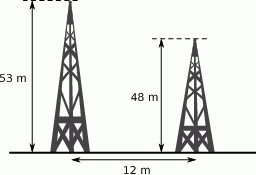
Dwa stalowe maszty o wysokościach 48 m i 53 m stoją w odległości 12 metrów od siebie. Czubki tych masztów postanowiono połączyć stalową liną, której 1 metr waży 500 g. Jaka będzie waga liny łączącej czubki masztów? Wynik podaj w kilogramach. Zapisz obliczenia.
Uzasadnij, że jeśli liczba jest podzielna przez 18 i przez 84, to jest podzielna przez 252.
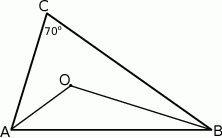
W trójkącie  , w którym
, w którym 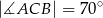 połączono środek okręgu wpisanego
połączono środek okręgu wpisanego 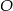 z wierzchołkami
z wierzchołkami 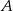 i
i 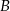 . Oblicz miarę kąta
. Oblicz miarę kąta 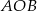 .
.