/Gimnazjum/Egzamin gimnazjalny/Egzamin 2013/Próbne testy
Próbny Egzamin Gimnazjalny
z Matematyki CKE 14 listopada 2012 Czas pracy: 90 minut
Do dzbanka wlano 2 jednakowe butelki soku.
Ile takich samych butelek wody należy dolać do dzbanka, aby sok stanowił 25% napoju? Wybierz odpowiedź spośród podanych.
A) 2 B) 4 C) 6 D) 8
Cztery pompy o jednakowej wydajności pracując jednocześnie, wypompowały wodę zgromadzoną w zbiorniku w czasie 12 godzin.
Ile takich pomp należałoby użyć, aby tę samą ilość wody wypompować w ciągu 6 godzin? Wybierz odpowiedź spośród podanych.
A) 2 B) 3 C) 6 D) 8
Korzystając z tego, że 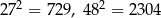 i
i 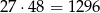 , oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
, oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
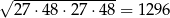 | P | F |
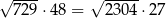 | P | F |
Dokończ zdanie tak, aby otrzymać zdanie prawdziwe.
Wyrażenie 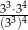 ma wartość
ma wartość
A) 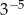 B)
B) 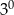 C)
C) 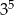 D)
D) 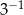
W pudełku znajduje się 6 losów, wśród których są 2 losy wygrywające.
Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
| Prawdopodobieństwo wyciągnięcia losu wygrywającego jest dwukrotnie mniejsze, niż wyciągnięcia losu przegrywającego. | P | F |
| Jeśli do pudełka włożymy dodatkowy los wygrywający, to prawdopodobieństwo wygranej wzrośnie. | P | F |
Na rysunku przedstawiono wykres pewnej funkcji.
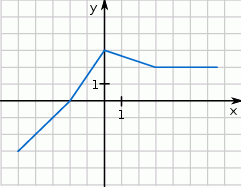
Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
Funkcja przyjmuje wartość 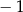 dla argumentu dla argumentu 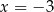 . . | P | F |
Dla wszystkich argumentów 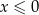 funkcja przyjmuje wartości ujemne. funkcja przyjmuje wartości ujemne. | P | F |
W pewnej kawiarni podaje się klientom dziennie średnio 70 filiżanek kawy. Ze 100 g ziarnistej kawy można przygotować 22 filiżanki tego napoju.
Ile co najmniej półkilogramowych paczek kawy musi kupić właściciel, aby wystarczyło jej na 7 dni? Wybierz odpowiedź spośród podanych.
A) 3 B) 4 C) 5 D) 6
Pan Nowak postanowił kupić wykładzinę na prostokątną podłogę o wymiarach 3 m i 4 m. Pod uwagę wziął dwa typy wykładziny.
| Typ wykładziny | Szerokość wykładziny | Cena wykładziny |
| welurowa | 4 m | 35 zł za 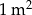 |
| wełniana | 3 m | 95 zł za 1 metr bieżący |
Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
Cena 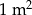 wykładziny welurowej jest niższa niż cena wykładziny welurowej jest niższa niż cena 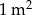 wykładziny wełnianej. wykładziny wełnianej. | P | F |
| Kupując tańszą wykładzinę, pan Nowak zaoszczędzi 40 zł. | P | F |
W jakim stosunku można podzielić odcinek o długości 36 cm, aby z otrzymanych trzech odcinków zbudować trójkąt? Wybierz odpowiedź spośród podanych.
A) 1 : 2 : 6 B) 1 : 3 : 5 C) 2 : 3 : 4 D) 2 : 3 : 7
Informacja do zadań 10 i 11
Zaczynając od punktu 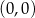 budujemy łamaną, której część składającą się z 10 odcinków przedstawiono na rysunku. Kolejne odcinki łamanej numerujemy kolejnymi liczbami naturalnymi. Pierwszy odcinek łamanej ma długość 1.
budujemy łamaną, której część składającą się z 10 odcinków przedstawiono na rysunku. Kolejne odcinki łamanej numerujemy kolejnymi liczbami naturalnymi. Pierwszy odcinek łamanej ma długość 1.
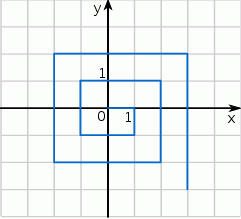
Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
Jeżeli  jest liczbą parzystą, to odcinek o numerze jest liczbą parzystą, to odcinek o numerze  jest równoległy do osi jest równoległy do osi 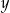 . . | P | F |
Jeżeli  jest liczbą nieparzystą, to długość odcinka o numerze jest liczbą nieparzystą, to długość odcinka o numerze  jest równa jest równa 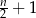 . . | P | F |
Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
| Łamana złożona z początkowych 7 odcinków ma długość 16. | P | F |
| Długość setnego odcinka łamanej jest równa 100. | P | F |
Do okręgu o środku 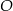 należą punkty
należą punkty 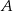 i
i 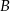 . Okrąg ma długość 54, a łuk
. Okrąg ma długość 54, a łuk 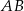 ma długość 18.
ma długość 18.
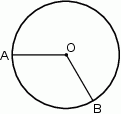
Jaką miarę ma kąt środkowy oparty na tym łuku?
Wybierz odpowiedź spośród podanych.
A) 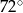 B)
B) 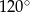 C)
C) 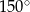 D)
D) 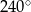
W układzie współrzędnych zaznaczono wierzchołki 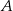 i
i 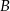 czworokąta
czworokąta 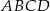 . Osie układu współrzędnych są osiami symetrii tego czworokąta.
. Osie układu współrzędnych są osiami symetrii tego czworokąta.
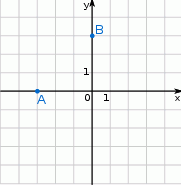
Dokończ zdanie tak, aby otrzymać zdanie prawdziwe. Pole czworokąta 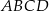 jest równe
jest równe
A) 9 B) 12 C) 18 D) 36
W trójkącie równoramiennym 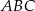 , w którym
, w którym 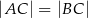 i
i 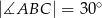 poprowadzono wysokość
poprowadzono wysokość 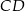 i dwusieczną kąta
i dwusieczną kąta 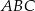 przecinającą bok
przecinającą bok 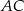 w punkcie
w punkcie 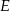 . Wysokość i dwusieczna przecinają się w punkcie
. Wysokość i dwusieczna przecinają się w punkcie 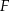 .
.
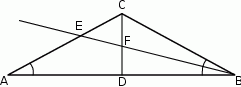
Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
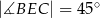 | P | F |
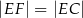 | P | F |
Dany jest trapez prostokątny 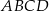 o podstawach długości 22 cm, 10 cm i wysokości 5 cm. Odcinek
o podstawach długości 22 cm, 10 cm i wysokości 5 cm. Odcinek 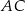 jest przekątną tego trapezu.
jest przekątną tego trapezu.
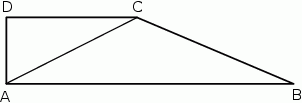
Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
Trójkąt 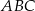 jest równoramienny. jest równoramienny. | P | F |
Bok 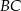 ma długość 12 cm. ma długość 12 cm. | P | F |
Z kwadratowego kartonika odcięto naroża, tak jak pokazano na rysunku i otrzymano ośmiokąt foremny o bokach długości 4.
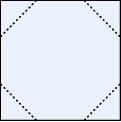
Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
| Kartonik był kwadratem o boku 12. | P | F |
| Suma pól odciętych naroży jest równa 16. | P | F |
Sześcian o objętości 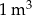 rozcięto na sześciany o krawędzi 1 cm. Gdyby wszystkie otrzymane sześciany ustawiono jeden za drugim, tak jak na rysunku, to powstałby prostopadłościan.
rozcięto na sześciany o krawędzi 1 cm. Gdyby wszystkie otrzymane sześciany ustawiono jeden za drugim, tak jak na rysunku, to powstałby prostopadłościan.
![]()
Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
| Jedna z krawędzi powstałego prostopadłościanu miałaby długość 10 km. | P | F |
| Objętość prostopadłościanu byłaby 100 razy większa od objętości początkowego sześcianu. | P | F |
Dwie proste równoległe 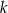 i
i 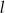 przecięto prostymi
przecięto prostymi 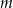 i
i  w sposób przedstawiony na rysunku.
w sposób przedstawiony na rysunku.
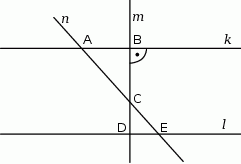
Czy trójkąty 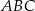 i
i 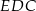 są podobne? Wybierz odpowiedź T albo N oraz jej uzasadnienie spośród zdań oznaczonych literami A–C.
są podobne? Wybierz odpowiedź T albo N oraz jej uzasadnienie spośród zdań oznaczonych literami A–C.
| Tak | Nie |
| ponieważ | |
| A) | te trójkąty mają wspólny wierzchołek. |
| B) | te trójkąty mają boki różnej długości. |
| C) | te trójkąty mają odpowiednie kąty równej miary. |
Który z poniższych rysunków nie może być siatką ostrosłupa prawidłowego czworokątnego? Wybierz odpowiedź spośród podanych.
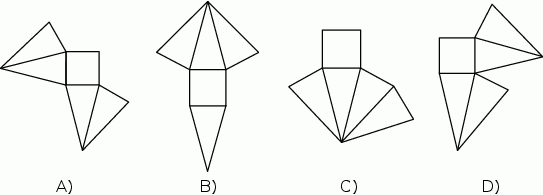
Dokończ zdanie tak, aby otrzymać zdanie prawdziwe.
Jeżeli długość każdej krawędzi podstawy ostrosłupa prawidłowego czworokątnego zwiększymy 2 razy, a jego wysokość zmniejszymy 2 razy, to objętość ostrosłupa
A) zwiększy się czterokrotnie. B) zwiększy się dwukrotnie.
C) zmniejszy się dwukrotnie. D) nie zmieni się.
Na zakup biletów do kina klasa 3a zebrała 360 zł, klasy 3b i 3c po 300 zł, a klasa 3d – 240 zł. Szkole udzielono rabatu i wszystkie bilety kosztowały 1000 zł. Uzyskany rabat podzielono między cztery klasy proporcjonalnie do zebranych kwot. Jaką kwotę zwrócono klasie 3a? Zapisz obliczenia.
Paweł rzucił 5 razy zwykłą sześcienną kostką do gry. Zapisane kolejno wyniki rzutów utworzyły liczbę pięciocyfrową. Liczba ta jest parzysta i podzielna przez 9, a jej początkowe trzy cyfry to: 3, 1, 2. Ile oczek wyrzucił Paweł za czwartym i piątym razem? Podaj wszystkie możliwości. Odpowiedź uzasadnij.
Pole powierzchni całkowitej graniastosłupa prawidłowego czworokątnego jest równe 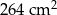 . Pole podstawy tej bryły stanowi 75% pola powierzchni jednej ściany bocznej. Oblicz wysokość bryły. Zapisz obliczenia.
. Pole podstawy tej bryły stanowi 75% pola powierzchni jednej ściany bocznej. Oblicz wysokość bryły. Zapisz obliczenia.

