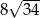/Szkoła średnia/Geometria/Planimetria/Czworokąt

Zadanie nr 1280893

Dodaj do ulubionych
Dodaj do rozwiązanych

Pole rombu jest równe 120. Gdyby zwiększyć długości jego przekątnych odpowiednio o 2 i 5 to pole wzrosłoby o 55. Oblicz obwód rombu. Podaj wszystkie możliwe odpowiedzi.

Rozwiązanie

Oznaczmy długości przekątnych rombu przez 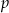p i q .

PIC

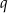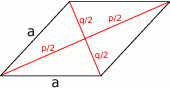
Zatem (ze wzoru na pole rombu z przekątnymi)

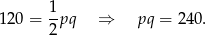
120 = 1pq ⇒ pq = 240 . 2

Wiemy ponadto, że

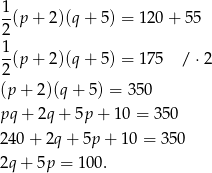
1 -(p + 2)(q + 5) = 120+ 55 2 1(p + 2)(q + 5) = 175 / ⋅2 2 (p + 2)(q+ 5) = 350 pq+ 2q+ 5p + 10 = 350 240+ 2q+ 5p + 10 = 350 2q+ 5p = 100 .

Podstawmy w tej równości 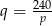240 q = -p- .

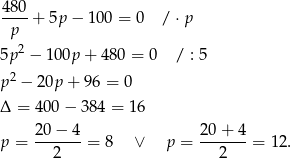
48 0 ----+ 5p − 100 = 0 / ⋅p p 5p 2 − 10 0p+ 480 = 0 / : 5 p2 − 20p + 96 = 0 Δ = 400 − 384 = 16 20-−-4- 2-0+-4- p = 2 = 8 ∨ p = 2 = 12.

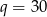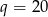Wtedy q = 3 0 i q = 20 odpowiednio.

Pozostało wyliczyć długość boku rombu. Ponieważ przekątne rombu są prostopadłe i dzielą się na połowy, na mocy twierdzenia Pitagorasa mamy

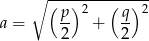
∘ (---)----(--)- p- 2 q- 2 a = 2 + 2

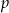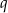Dla wyliczonych wartości p i q otrzymujemy odpowiednio

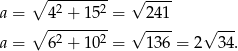
∘ --------- √ ---- a = 42 + 152 = 241 ∘ --------- √ ---- √ --- a = 62 + 102 = 136 = 2 3 4.

Zatem obwód rombu jest równy odpowiednio 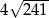√ ---- 4 24 1 i √ --- 8 34 .  
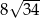Odpowiedź: 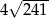---- 4√ 24 1 lub 8√ 3-4

Wersja PDF