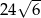/Szkoła średnia/Geometria/Planimetria/Czworokąt

Zadanie nr 1992164

Dodaj do ulubionych
Dodaj do rozwiązanych

Wysokość trapezu równoramiennego ma długość 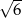√ -- 6 , a jedna z podstaw jest trzy razy dłuższa od drugiej. Oblicz pole trapezu wiedząc, że sinus jego kąta ostrego jest równy 0,2.

Rozwiązanie

Zaczynamy od rysunku – jeżeli poprowadzimy obie wysokości trapezu, to z podanych informacji dzielą one dłuższą podstawę na trzy równe części.

PIC

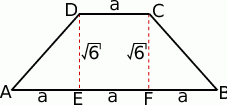
Aby móc wykorzystać podaną informację o sinusie kąta 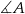∡A , policzmy długość przeciwprostokątnej w trójkącie prostokątnym AED .

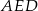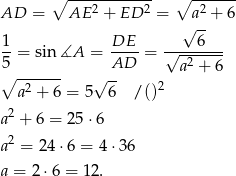
∘ ------------ ∘ ------ AD = AE 2 + ED 2 = a2 + 6 √ -- 1-= sin ∡A = DE-- = √----6--- 5 AD a2 + 6 ∘ ------ √ -- 2 a2 + 6 = 5 6 /() a2 + 6 = 25 ⋅6 a2 = 24 ⋅6 = 4 ⋅36 a = 2 ⋅6 = 12 .

Możemy teraz obliczyć pole

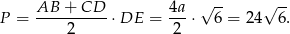
AB + CD 4a √ -- √ -- P = ----------⋅ DE = ---⋅ 6 = 24 6. 2 2

 
Odpowiedź: √ -- 24 6

Wersja PDF