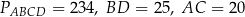/Szkoła średnia/Geometria/Planimetria/Czworokąt

Zadanie nr 2074631

Dodaj do ulubionych
Dodaj do rozwiązanych

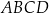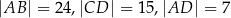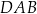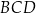W czworokącie ABCD dane są długości boków: |AB | = 24,|CD | = 1 5,|AD | = 7 . Ponadto kąty DAB oraz BCD są proste. Oblicz pole tego czworokąta oraz długości jego przekątnych.

Rozwiązanie

Zaczynamy od szkicowego rysunku.

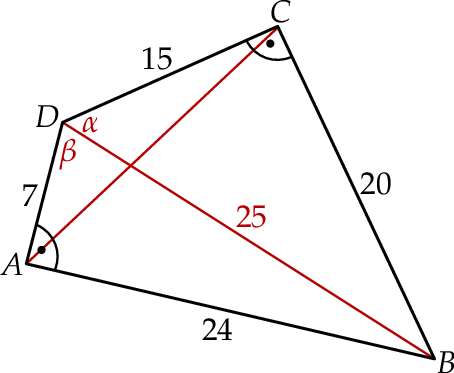
ZINFO-FIGURE

Z trójkąta prostokątnego 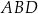ABD liczymy długość przekątnej BD .

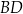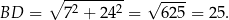
∘ --------- √ ---- BD = 72 + 242 = 6 25 = 25.

Teraz z trójkąta prostokątnego 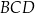BCD liczymy długość boku BC .

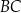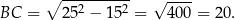
∘ ---------- √ ---- BC = 25 2 − 15 2 = 400 = 2 0.

Teraz bez trudu liczymy pole czworokąta.

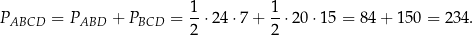
1 1 PABCD = PABD + PBCD = -⋅ 24⋅7 + -⋅ 20⋅1 5 = 84 + 150 = 234. 2 2

Pozostało obliczyć długość drugiej przekątnej – zrobimy to na dwa sposoby.

Sposób I

Długość przekątnej 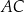AC obliczymy stosując twierdzenie cosinusów w trójkącie 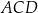ACD . Zanim to jednak zrobimy obliczymy 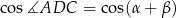cos∡ADC = cos(α+ β) . Korzystamy ze wzoru na cosinus sumy.

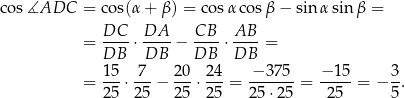
cos ∡ADC = cos(α + β ) = cosα cos β− sin α sin β = = DC--⋅ DA--− CB--⋅ AB-= DB DB DB DB 15- 7-- 20- 2-4 -−-375- −-15- 3- = 25 ⋅ 25 − 25 ⋅2 5 = 25 ⋅25 = 25 = − 5.

Liczymy teraz długość przekątnej 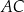AC .

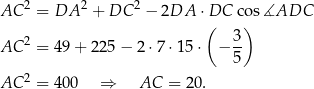
AC 2 = DA 2 + DC 2 − 2DA ⋅DC cos ∡ADC ( 3 ) AC 2 = 49 + 225 − 2 ⋅7 ⋅15⋅ − -- 5 AC 2 = 400 ⇒ AC = 20.

Sposób II

Ponieważ czworokąt 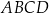ABCD jest wpisany w okrąg (średnicą tego okręgu jest odcinek 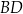BD ), możemy skorzystać z twierdzenia Ptolemeusza.

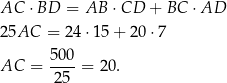
AC ⋅BD = AB ⋅CD + BC ⋅AD 25AC = 24 ⋅15 + 20 ⋅7 500 AC = ----= 20. 25

 
Odpowiedź: PABCD = 234, BD = 25 , AC = 20

Wersja PDF