Zadanie nr 2185792
Na bokach 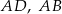 i
i 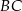 rombu
rombu 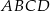 wybrano punkty
wybrano punkty 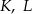 i
i 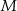 w ten sposób, że
w ten sposób, że 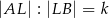 oraz
oraz 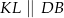 ,
, 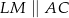 . Wyznacz wszystkie wartości
. Wyznacz wszystkie wartości 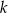 , dla których pole pięciokąta
, dla których pole pięciokąta 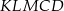 stanowi
stanowi 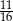 pola rombu.
pola rombu.
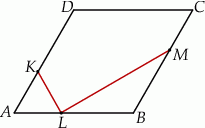
Rozwiązanie
Oznaczmy pole rombu przez 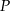 . Oczywiście wystarczy sprawdzić, kiedy pola trójkątów
. Oczywiście wystarczy sprawdzić, kiedy pola trójkątów 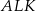 i
i 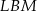 w sumie stanowią
w sumie stanowią 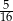 pola rombu.
pola rombu.
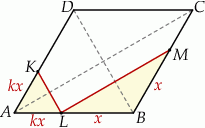
Po pierwsze zauważmy, że z równoległości 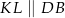 wynika, że trójkąty
wynika, że trójkąty 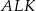 i
i 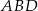 są podobne. W szczególności stosunek ich pól jest równy
są podobne. W szczególności stosunek ich pól jest równy
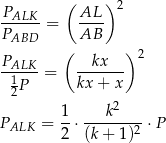
Analogicznie uzasadniamy, że trójkąty 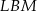 i
i 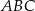 są podobne oraz
są podobne oraz
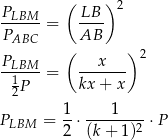
Pozostało więc rozwiązać równanie
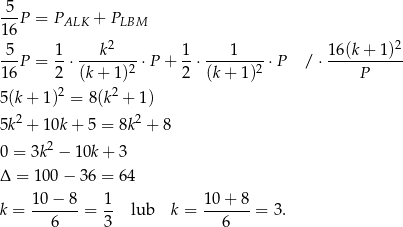
Odpowiedź: 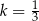 lub
lub