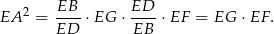Zadanie nr 2235986
Prosta przechodząca przez wierzchołek  równoległoboku
równoległoboku  przecina jego przekątną
przecina jego przekątną  w punkcie
w punkcie 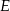 i bok
i bok 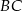 w punkcie
w punkcie 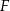 , a prostą
, a prostą 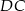 w punkcie
w punkcie 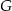 . Udowodnij, że
. Udowodnij, że
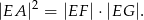
Rozwiązanie
Rozpoczynamy od szkicowego rysunku.
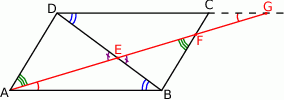
Zauważmy, że mamy dwie pary trójkątów podobnych:  i
i 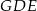 oraz
oraz 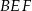 i
i 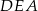 (są podobne, bo mają równe kąty). Z pierwszego podobieństwa mamy
(są podobne, bo mają równe kąty). Z pierwszego podobieństwa mamy
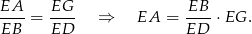
Z drugiego podobieństwa
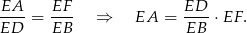
Mnożąc te dwie równości stronami mamy