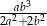Zadanie nr 2347515
Dany jest prostokąt 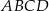 , w którym
, w którym 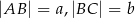 i
i 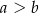 . Odcinek
. Odcinek 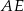 jest wysokością trójkąta
jest wysokością trójkąta 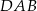 opuszczoną na jego bok
opuszczoną na jego bok 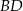 . Wyraź pole trójkąta
. Wyraź pole trójkąta 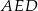 za pomocą
za pomocą  i
i 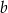 .
.
Rozwiązanie
Rozpoczynamy od rysunku.
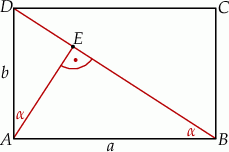
Sposób I
Zauważmy, że trójkąty prostokątne 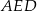 i
i 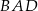 są podobne (bo mają wspólny kąt
są podobne (bo mają wspólny kąt 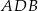 ). Znamy ponadto ich skalę podobieństwa
). Znamy ponadto ich skalę podobieństwa
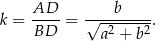
Ponieważ pole zmienia się jak kwadrat skali podobieństwa, mamy
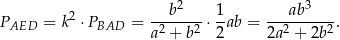
Sposób II
Liczymy długość przekątnej prostokąta.
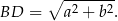
Zauważmy, że
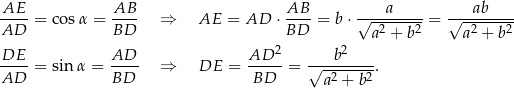
Obliczamy pole trójkąta 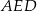 .
.
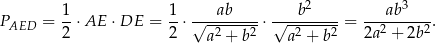
Odpowiedź: