/Szkoła średnia/Geometria/Planimetria/Czworokąt

Zadanie nr 2424990

Dodaj do ulubionych
Dodaj do rozwiązanych

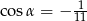Dany jest czworokąt o kolejnych bokach długości 3,4,5 oraz kącie α między bokami długości 3 i 4 takim, że cosα = − 111 . Wyznacz długość czwartego boku, jeśli wiadomo, że na czworokącie można opisać okrąg.

Rozwiązanie

Zaczynamy od rysunku.

PIC

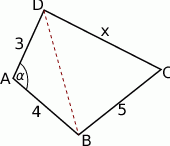
Obliczmy najpierw długość przekątnej 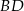BD (z twierdzenia cosinusów)

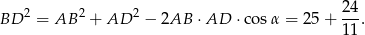
BD 2 = AB 2 + AD 2 − 2AB ⋅AD ⋅co sα = 25+ 24. 11

Ponieważ w czworokącie wpisanym w okrąg sumy przeciwległych kątów są równe 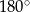18 0∘ , więc 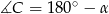∡C = 180∘ − α . W szczególności

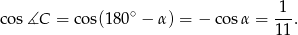
cos∡C = cos(180∘ − α) = − cos α = -1-. 11

Możemy teraz napisać twierdzenie cosinusów w trójkącie 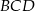BCD .

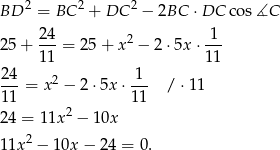
2 2 2 BD = BC + DC − 2BC ⋅DC cos ∡C 24- 2 1-- 25 + 11 = 25 + x − 2 ⋅5x ⋅11 24 1 ---= x2 − 2⋅ 5x⋅ --- /⋅ 11 11 11 24 = 11x 2 − 10x 2 11x − 10x − 2 4 = 0.

Liczymy dalej,

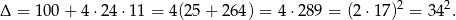
2 2 Δ = 100 + 4⋅ 24⋅ 11 = 4(25 + 264 ) = 4⋅ 289 = (2 ⋅17) = 34 .

Stąd dodatni pierwiastek to 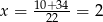x = 10+34 = 2 22 .  
Odpowiedź: 2

Wersja PDF