/Szkoła średnia/Geometria/Planimetria/Czworokąt

Zadanie nr 3116014

Dodaj do ulubionych
Dodaj do rozwiązanych

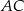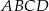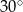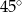Przekątna AC równoległoboku ABCD tworzy z jego bokami kąty o miarach 30 ∘ i 45∘ . Oblicz stosunek 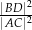2 |BD|2 |AC| kwadratów długości przekątnych tego równoległoboku.

Rozwiązanie

Oznaczmy długości boków równoległoboku przez a i b .

PIC

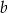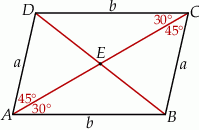
Na mocy twierdzenia sinusów w trójkącie 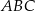ABC mamy

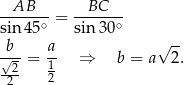
--AB--- = -BC---- sin 45∘ sin 30∘ -b- a- √ -- √2-= 1 ⇒ b = a 2. 2 2

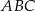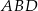Długości przekątnych obliczymy korzystając z twierdzenia cosinusów w trójkątach ABC i ABD . Zanim to jednak zrobimy obliczmy potrzebne do tego cosinusy.

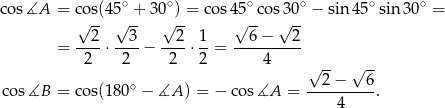
co s∡A = cos(45∘ + 30∘) = co s45∘ cos30 ∘ − sin 45∘sin 30∘ = √ -- √ -- √ -- √ -- √ -- = --2-⋅--3-− --2⋅ 1-= --6−----2- 2 2 2 2 4 √ -- √ -- 2− 6 cos∡B = cos(180∘ − ∡A ) = − cos ∡A = ---------. 4

Obliczamy teraz długości przekątnych

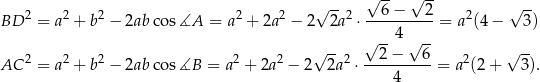
√ -- √ -- 2 2 2 2 2 √ --2 --6-−---2- 2 √ -- BD = a + b − 2ab cos∡A = a + 2a − 2 2a ⋅ 4 = a (4− 3) √ -- √ 2-− √ 6- √ -- AC 2 = a2 + b2 − 2ab cos∡B = a2 + 2a2 − 2 2a2 ⋅----------= a 2(2+ 3). 4

Interesujący nas stosunek jest więc równy

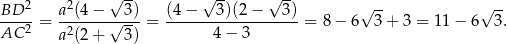
√ -- √ -- √ -- BD 2 a2(4 − 3) (4 − 3)(2 − 3) √ -- √ -- ----2 = -2-----√----= -------------------= 8− 6 3+ 3 = 11 − 6 3. AC a (2 + 3) 4− 3

 
Odpowiedź: 11 − 6√ 3-

Wersja PDF