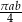/Szkoła średnia/Geometria/Planimetria/Czworokąt

Zadanie nr 3389596

Dodaj do ulubionych
Dodaj do rozwiązanych

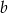Trapez równoramienny o podstawach długości a i b opisany jest na okręgu. Oblicz pole koła, którego brzegiem jest okrąg wpisany w ten trapez.

Rozwiązanie

Zaczynamy od rysunku.

PIC

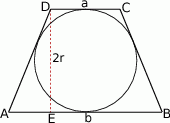
Spróbujmy na początek obliczyć promień okręgu wpisanego w trapez. Ponieważ w trapez można wpisać okrąg, to

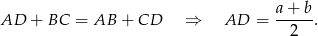
AD + BC = AB + CD ⇒ AD = a+--b. 2

Ponadto

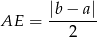
AE = |b−--a| 2

(Dodaliśmy wartość bezwzględną, bo nie wiemy, czy 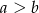a > b , czy też 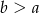b > a ). Napiszmy teraz twierdzenie Pitagorasa w trójkącie AED .

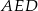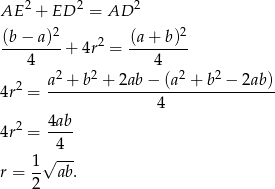
AE 2 + ED 2 = AD 2 (b − a)2 (a+ b)2 -------- + 4r2 = -------- 4 4 2 a2 +-b-2 +-2ab-−-(a-2 +-b2-−-2ab-) 4r = 4 4r2 = 4ab- 4 1√ --- r = 2 ab.

Zatem pole koła wynosi

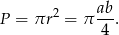
ab P = πr 2 = π ---. 4

 
Odpowiedź: πab 4

Wersja PDF