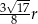/Szkoła średnia/Geometria/Planimetria/Czworokąt

Zadanie nr 3548933

Dodaj do ulubionych
Dodaj do rozwiązanych

Punkt styczności okręgu o promieniu r wpisanego w trapez równoramienny dzieli ramię trapezu w stosunku 1:2. Oblicz promień okręgu opisanego na tym trapezie.

Rozwiązanie

Zacznijmy od rysunku i oznaczmy 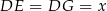DE = DG = x .

PIC

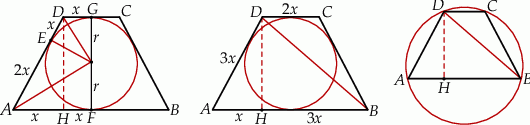
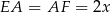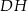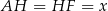Z podanych informacji wiemy, że EA = AF = 2x . W takim razie, prowadząc wysokość DH mamy AH = HF = x . Stosujemy teraz twierdzenie Pitagorasa do trójkąta AHD .

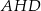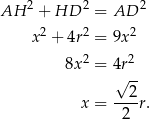
AH 2 + HD 2 = AD 2 2 2 2 x + 4r = 9x 8x2 = 4r2 √ -- --2- x = 2 r.

Zastanówmy się teraz co mamy obliczyć. Okrąg opisany na trapezie jest w szczególności opisany na trójkącie 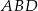ABD , możemy więc obliczyć jego promień 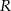R z twierdzenia sinusów.

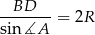
BD -------= 2R sin ∡A

Z sinusem nie ma problemu

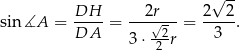
√ -- DH 2r 2 2 sin ∡A = ----= ---√--- = -----. DA 3 ⋅-22r 3

Co do przekątnej 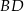BD , to obliczamy ją z trójkąta prostokątnego DHB .

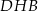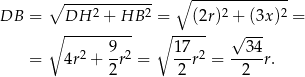
∘ ------------- ∘ -------------- DB = DH 2 + HB 2 = (2r)2 + (3x )2 = ∘ ---------- ∘ ----- √ --- = 4r2 + 9r2 = 17r2 = --34r. 2 2 2

Mamy zatem

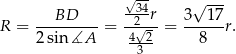
√ -- √ --- BD -234r 3 17 R = 2sin-∡A--= 4√-2-= --8---r. --3-

 
Odpowiedź: √ -- 3--17r 8

Wersja PDF