Zadanie nr 3605721
Długość boku rombu jest równa  , a długości jego przekątnych są równe
, a długości jego przekątnych są równe 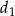 i
i 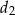 . Oblicz miarę kąta ostrego rombu jeżeli wiadomo, że
. Oblicz miarę kąta ostrego rombu jeżeli wiadomo, że 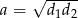 .
.
Rozwiązanie
Rozpoczynamy od szkicowego rysunku.
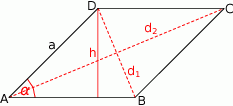
Sposób I
Korzystamy z dwóch wzorów na pole rombu: ze wzoru z sinusem i ze wzoru z przekątnymi.
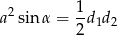
Korzystamy teraz z podanego warunku 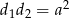 .
.
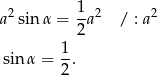
Zatem 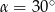 .
.
Sposób II
Korzystamy z dwóch wzorów na pole rombu: ze wzoru z przekątnymi i ze wzoru z wysokością.
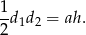
Korzystamy teraz z podanego warunku 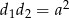 .
.
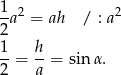
Zatem 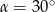 .
.
Odpowiedź: