Zadanie nr 3666241
Środek okręgu wpisanego w trapez prostokątny, znajduje się w odległości 4 oraz 8 od końców dłuższego ramienia trapezu. Oblicz pole tego trapezu.
Rozwiązanie
Zacznijmy od rysunku.
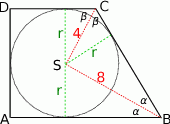
Zauważmy, że trójkąty prostokątne, których jeden bok jest promieniem okręgu wpisanego, a przeciwprostokątną jest 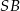 , są przystające. Zatem prosta
, są przystające. Zatem prosta 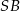 jest dwusieczną kąta
jest dwusieczną kąta 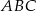 . Oznaczmy kąty na jakie dzieli ona kąt
. Oznaczmy kąty na jakie dzieli ona kąt 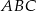 przez
przez  . Podobnie niech
. Podobnie niech 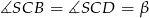 . Z równoległości prostych
. Z równoległości prostych 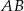 i
i 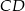 mamy
mamy
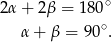
Oznacza to, że trójkąt 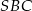 jest prostokątny. Na mocy twierdzenia Pitagorasa
jest prostokątny. Na mocy twierdzenia Pitagorasa
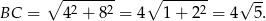
Możemy teraz łatwo wyliczyć promień okręgu wpisanego – jest to wysokość w trójkącie 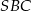 opuszczona na bok
opuszczona na bok 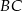 .
.
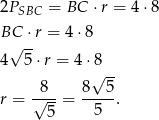
Innym sposobem wyliczenia promienia jest fakt, że 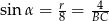 .
.
Mamy zatem wysokość trapezu
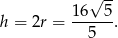
Długości podstaw możemy teraz wyliczyć z twierdzenia Pitagorasa w odpowiednich trójkątach. My jednak zrobimy to prościej. Ponieważ trapez jest opisany na okręgu, to
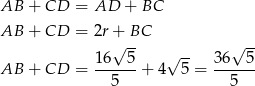
Mamy stąd
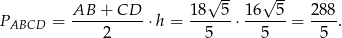
Odpowiedź: