/Szkoła średnia/Geometria/Planimetria/Czworokąt

Zadanie nr 3698597

Dodaj do ulubionych
Dodaj do rozwiązanych

W równoległoboku, który nie jest prostokątem, krótsza przekątna dzieli go na dwa równoramienne trójkąty prostokątne. Krótszy bok równoległoboku ma długość 8. Oblicz pole tego równoległoboku.

Rozwiązanie

Rozpoczynamy od szkicowego rysunku.

PIC

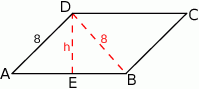
Na mocy twierdzenia Pitagorasa w trójkącie 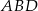ABD (lub wzoru na długość przekątnej kwadratu) mamy

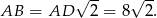
√ -- √ -- AB = AD 2 = 8 2.

Sposób I

Trójkąt 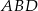ABD jest połówką kwadratu, zatem

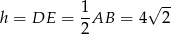
1 √ -- h = DE = --AB = 4 2 2

i pole równoległoboku jest równe

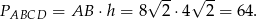
P = AB ⋅h = 8√ 2-⋅4√ 2-= 64. ABCD

Sposób II

Zauważmy, że trójkąt 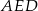AED jest prostokątny i równoramienny (bo 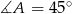∡A = 45∘ ). Zatem

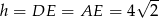
√ -- h = DE = AE = 4 2

i pole równoległoboku jest równe

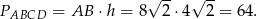
√ -- √ -- PABCD = AB ⋅h = 8 2 ⋅4 2 = 64.

 
Odpowiedź: 64

Wersja PDF