/Szkoła średnia/Geometria/Planimetria/Czworokąt

Zadanie nr 3995958

Dodaj do ulubionych
Dodaj do rozwiązanych

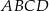Trapez ABCD jest wpisany w okrąg, przekątna 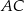AC jest zawarta w dwusiecznej kąta 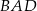BAD , a długość podstawy 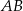AB jest dwa razy większa niż długość podstawy 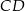CD . Oblicz pole trapezu i obwód wiedząc że jego wysokość jest równa √ 3- .

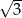Rozwiązanie

Oznaczmy 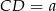CD = a .

PIC

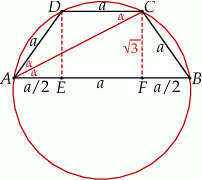
Trapez wpisany w okrąg jest zawsze równoramienny, ponadto

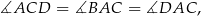
∡ACD = ∡BAC = ∡DAC ,

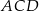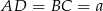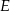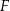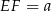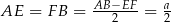więc trójkąt ACD jest równoramienny. Mamy stąd AD = BC = a . Jeżeli ponadto E i F są spodkami wysokości trapezu, to EF = a i AE = FB = AB-−EF-= a 2 2 .

Piszemy teraz twierdzenie Pitagorasa w trójkącie 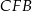CF B .

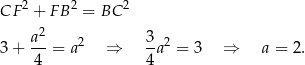
CF 2 + FB 2 = BC 2 a2- 2 3- 2 3 + 4 = a ⇒ 4a = 3 ⇒ a = 2.

Obwód trapezu jest więc równy 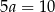5a = 10 , a jego pole to

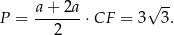
P = a+--2a-⋅CF = 3√ 3. 2

 
Odpowiedź: Obwód: 10, pole: 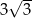√ -- 3 3 .

Wersja PDF