Zadanie nr 4154193
Dany jest kwadrat 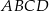 . Przekątne
. Przekątne 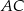 i
i 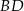 przecinają się w punkcie
przecinają się w punkcie 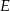 . Punkty
. Punkty 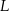 i
i 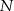 są środkami odcinków – odpowiednio –
są środkami odcinków – odpowiednio – 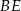 i
i 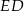 . Punkty
. Punkty 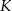 i
i 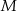 leżą na przekątnej
leżą na przekątnej 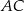 tak, że
tak, że 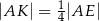 i
i 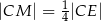 (zobacz rysunek). Wykaż, że stosunek pola czworokąta
(zobacz rysunek). Wykaż, że stosunek pola czworokąta 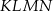 do pola kwadratu
do pola kwadratu 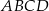 jest równy 3:8.
jest równy 3:8.
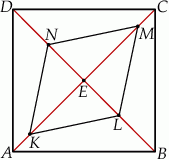
Rozwiązanie
Sposób I
Korzystamy z tego, że przekątne kwadratu są prostopadłe.
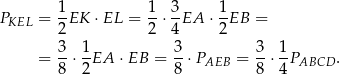
Dokładnie w ten sam sposób uzasadniamy, że
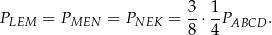
Mamy zatem
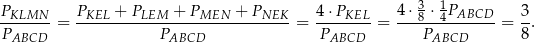
Sposób II
Korzystamy ze wzoru na pole rombu z przekątnymi.