/Szkoła średnia/Geometria/Planimetria/Czworokąt

Zadanie nr 4208886

Dodaj do ulubionych
Dodaj do rozwiązanych

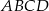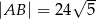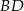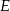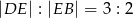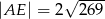Dany jest prostokąt ABCD , w którym √ -- |AB | = 24 5 . Na przekątnej BD leży punkt E taki, że |DE | : |EB | = 3 : 2 oraz √ ---- |AE | = 2 2 69 . Oblicz pole prostokąta ABCD .

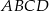Rozwiązanie

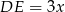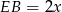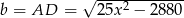Oznaczmy DE = 3x , EB = 2x oraz √ ----2------- b = AD = 2 5x − 2880 .

PIC

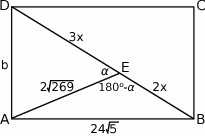
Oznaczmy 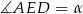∡AED = α . Wtedy oczywiście 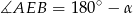∡AEB = 180∘ − α . Piszemy teraz twierdzenia cosinusów w trójkątach 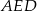AED i AEB .

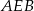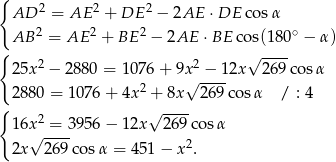
{ AD 2 = AE 2 + DE 2 − 2AE ⋅DE cosα 2 2 2 ∘ { AB = AE + BE − 2AE ⋅BE co s(180 − α) 25x2 − 2880 = 1076 + 9x2 − 12x √ 269-cosα √ ---- 2880 = 1 076+ 4x2 + 8x 2 69cos α / : 4 { 2 √ ---- 16x√ -=-39 56− 12x 26 9cos α 2x 269 cos α = 451 − x2.

Podstawiamy teraz 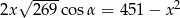√ ---- 2 2x 2 69cos α = 45 1− x z drugiego równania do pierwszego.

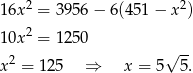
2 2 16x = 39 56− 6(451 − x ) 10x2 = 12 50 2 √ -- x = 125 ⇒ x = 5 5.

W takim razie

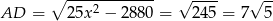
∘ ------------ √ ---- √ -- AD = 25x2 − 2880 = 245 = 7 5

i pole prostokąta jest równe

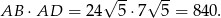
√ -- √ -- AB ⋅AD = 24 5 ⋅7 5 = 840 .

 
Odpowiedź: 840

Wersja PDF