Zadanie nr 4252657
Podstawy trapezu prostokątnego mają długości 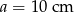 i
i 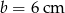 , zaś bok prostopadły do podstaw ma długość
, zaś bok prostopadły do podstaw ma długość 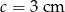 .
.
- Oblicz odległość punktu przecięcia się przekątnych tego trapezu od podstawy długości
 i ramienia długości
i ramienia długości  .
. - Czy w trapez można wpisać okrąg? Odpowiedź uzasadnij.
Rozwiązanie
Zaczynamy od rysunku.
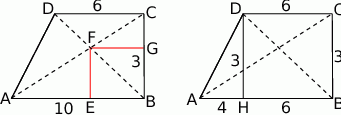
- Zauważmy, że trójkąty
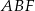 i
i 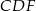 są podobne (bo mają równe kąty). W dodatku znamy skalę podobieństwa
są podobne (bo mają równe kąty). W dodatku znamy skalę podobieństwa 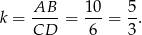
Zatem odcinek
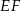 stanowi
stanowi  odcinka
odcinka 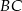 , czyli
, czyli 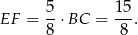
Podobnie jak poprzednio, ponieważ
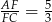 , więc
, więc 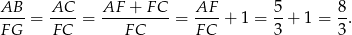
Czyli
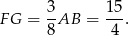
Odpowiedź: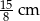 i
i 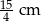
- W czworokąt można wpisać okrąg jeżeli sumy przeciwległych boków są równe. Aby sprawdzić czy tak jest, wyliczamy długość ramienia
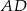 . Patrzymy na trójkąt prostokątny
. Patrzymy na trójkąt prostokątny 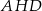 .
. 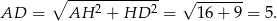
Zatem
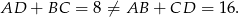
Odpowiedź: Nie, nie można.

