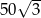Zadanie nr 4267355
W trapezie równoramiennym o podstawach długości 20 i 40, oraz kącie ostrym o mierze 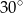 połączono środki wszystkich boków. Oblicz pole otrzymanego czworokąta.
połączono środki wszystkich boków. Oblicz pole otrzymanego czworokąta.
Rozwiązanie
Zaczynamy od rysunku.
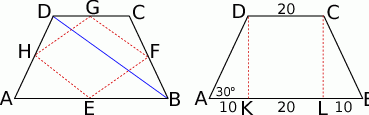
Od razu widać, że z trójkąta 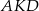 można wyliczyć długości wysokości i ramienia trapezu.
można wyliczyć długości wysokości i ramienia trapezu.
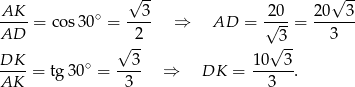
Sposób I
Zamiast liczyć pole czworokąta, łatwo można policzyć pola trójkątów, które do niego nie należą. Ponieważ 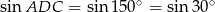 , więc suma tych pól jest równa
, więc suma tych pól jest równa
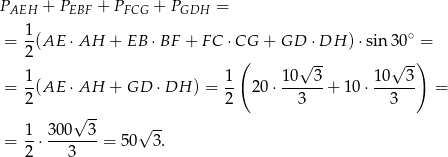
Aby otrzymać interesujące na pole czworokąta, musimy to pole trójkątów odjąć od pola trapezu.
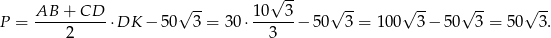
Sposób II
Jeżeli popatrzymy na trójkąty 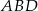 i
i 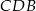 to z twierdzenia Talesa, dostajemy
to z twierdzenia Talesa, dostajemy 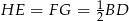 . Podobnie zauważamy, że
. Podobnie zauważamy, że 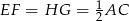 . Zatem interesujący nas czworokąt jest rombem i jego pole jest równe połowie iloczynu długości przekątnych. Przekątną
. Zatem interesujący nas czworokąt jest rombem i jego pole jest równe połowie iloczynu długości przekątnych. Przekątną 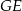 mamy już wyliczoną, a druga przekątna to odcinek łączący środki ramion trapezu, więc ma długość (znany fakt)
mamy już wyliczoną, a druga przekątna to odcinek łączący środki ramion trapezu, więc ma długość (znany fakt)
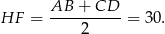
Zatem szukane pole jest równe
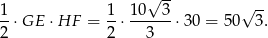
Sposób III
Jak zauważyliśmy w poprzednim sposobie 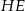 łączy środki boków w trójkącie
łączy środki boków w trójkącie 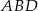 . Podobnie
. Podobnie 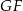 łączy środki boków w trójkącie
łączy środki boków w trójkącie 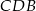 . Zatem
. Zatem
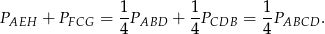
Podobnie uzasadniamy, że
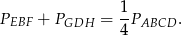
Zatem pole interesującego na czworokąta jest równe
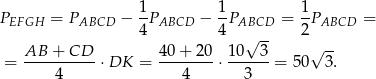
Odpowiedź: