Zadanie nr 4279347
W trapezie 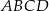 dane są długości podstaw:
dane są długości podstaw: 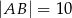 ,
, 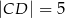 i ramion:
i ramion: 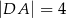 ,
, 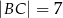 . Oblicz długość przekątnej
. Oblicz długość przekątnej 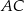 tego trapezu.
tego trapezu.
Rozwiązanie
Rozpoczynamy od szkicowego rysunku.
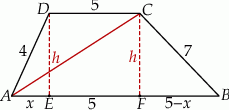
Sposób I
Oznaczmy 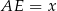 . Piszemy twierdzenia Pitagorasa w trójkątach
. Piszemy twierdzenia Pitagorasa w trójkątach 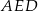 i
i 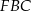 .
.
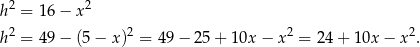
Porównujemy teraz 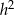 z obu równości.
z obu równości.
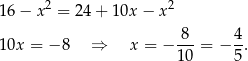
Otrzymana ujemna długość odcinka 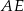 może wyglądać podejrzanie, ale tak naprawdę wszystko jest ok, ten rachunek próbuje nam po prostu powiedzieć, że wykonaliśmy zły rysunek - przy danych długościach boków trapezu punkt
może wyglądać podejrzanie, ale tak naprawdę wszystko jest ok, ten rachunek próbuje nam po prostu powiedzieć, że wykonaliśmy zły rysunek - przy danych długościach boków trapezu punkt 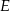 znajduje się na lewo od wierzchołka
znajduje się na lewo od wierzchołka 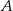 . Dokładnie tyle mówi nam ten wynik.
. Dokładnie tyle mówi nam ten wynik.
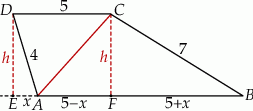
Łatwo sprawdzić, że przy poprawnym rysunku, otrzymamy 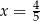 . Obliczamy teraz długość przekątnej – tak naprawdę wszystko którego rysunku i odpowiadającej wartości
. Obliczamy teraz długość przekątnej – tak naprawdę wszystko którego rysunku i odpowiadającej wartości  użyjemy – wynik będzie ten sam. My patrzymy na drugi rysunek i bierzemy
użyjemy – wynik będzie ten sam. My patrzymy na drugi rysunek i bierzemy 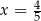 .
.
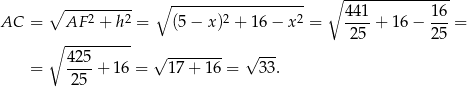
Sposób II
Tym razem użyjemy twierdzenia cosinusów.
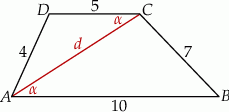
Oznaczmy 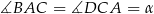 i napiszmy twierdzenia cosinusów w trójkątach
i napiszmy twierdzenia cosinusów w trójkątach 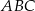 i
i 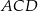 .
.
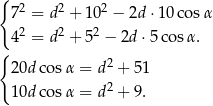
Odejmujemy teraz od pierwszego równania drugie pomnożone przez 2 i mamy
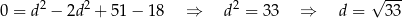
Sposób III
Tym razem umieśćmy trapez w układzie współrzędnych. Bez zmniejszania ogólności możemy założyć, że 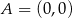 ,
, 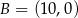 ,
, 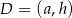 i
i 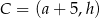 . Podane długości ramion prowadzą w takiej sytuacji do równości
. Podane długości ramion prowadzą w takiej sytuacji do równości
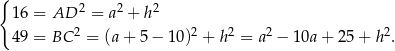
Jeżeli odejmiemy od drugiego równania pierwsze to mamy

Obliczamy długość przekątnej
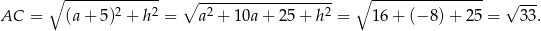
Odpowiedź: