/Szkoła średnia/Geometria/Planimetria/Czworokąt

Zadanie nr 4303700

Dodaj do ulubionych
Dodaj do rozwiązanych

Obwód rombu wynosi 68 cm, a długość jednej z jego przekątnych stanowi 187,5% długości drugiej przekątnej. Oblicz pole tego rombu.

Rozwiązanie

Szkicujemy romb.

PIC

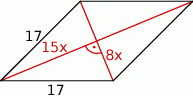
Wiemy, że stosunek długości przekątnych jest równy

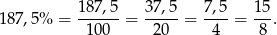
187,5% = 187,5-= 37,5-= 7,5-= 15. 100 20 4 8

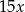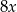Więc możemy oznaczyć połowy długości przekątnych przez 15x i 8x . Na mocy twierdzenia Pitagorasa mamy więc

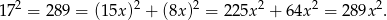
1 72 = 289 = (1 5x)2 + (8x)2 = 225x 2 + 64x2 = 28 9x2.

Mamy stąd 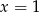x = 1 i pole rombu jest równe

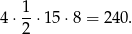
4⋅ 1-⋅15 ⋅8 = 240. 2

 
Odpowiedź: 240 cm 2

Wersja PDF