/Szkoła średnia/Geometria/Planimetria/Czworokąt

Zadanie nr 4346831

Dodaj do ulubionych
Dodaj do rozwiązanych

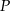Punkt P należy do okręgu opisanego na kwadracie 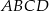ABCD . Wykaż, że wyrażenie 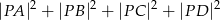|PA |2 + |P B|2 + |PC |2 + |PD |2 ma stałą wartość, niezależną od wyboru punktu P .

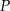Rozwiązanie

Sposób I

Zacznijmy od rysunku.

PIC

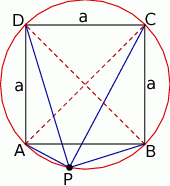
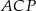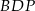Jeżeli dorysujemy przekątne kwadratu (a więc średnice okręgu), to trójkąty ACP i BDP są prostokątne. Zatem

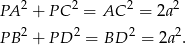
2 2 2 2 PA + PC = AC = 2a P B2 + PD 2 = BD 2 = 2a2.

Dodając te równości stronami mamy

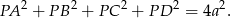
2 2 2 2 2 PA + PB + PC + P D = 4a .

Sposób II

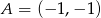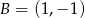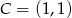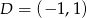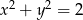Możemy tak wybrać układ współrzędnych na płaszczyźnie, że dany kwadrat ma wierzchołki A = (− 1,− 1) , B = (1,− 1) , C = (1,1) i D = (− 1,1) . Okrąg opisany na tym kwadracie ma równanie 2 2 x + y = 2 .

PIC

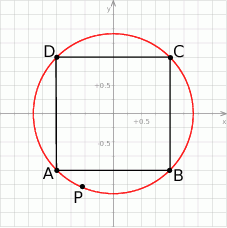
Jeżeli teraz 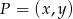P = (x,y) jest dowolnym punktem na okręgu, to

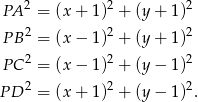
PA 2 = (x + 1)2 + (y + 1)2 2 2 2 PB = (x − 1) + (y + 1) 2 2 2 PC = (x − 1) + (y − 1) P D 2 = (x + 1)2 + (y − 1)2.

Dodając te równości stronami mamy

PA 2 + PB 2 + P C 2 + P D 2 = 4(x2 + y2) + 4+ 4 = 16.
Wersja PDF