/Szkoła średnia/Geometria/Planimetria/Czworokąt

Zadanie nr 4481041

Dodaj do ulubionych
Dodaj do rozwiązanych

W równoległoboku 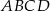ABCD kąt ostry 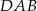DAB ma miarę 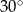∘ 30 , zaś dłuższy bok ma długość 8. Promień okręgu opisanego na trójkącie 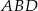ABD ma długość 4. Oblicz pole równoległoboku.

Rozwiązanie

Rozpoczynamy od rysunku.

PIC

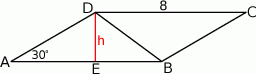
Widać, że dość łatwo jest wyliczyć długość przekątnej 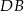DB – stosujemy twierdzenie sinusów

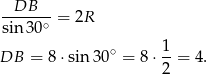
--DB--- = 2R sin30 ∘ ∘ 1 DB = 8 ⋅sin3 0 = 8 ⋅--= 4 . 2

Sposób I

W trójkącie 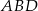ABD znamy długości dwóch boków oraz miarę jednego kąta. W takiej sytuacji możemy wyliczyć długość trzeciego boku z twierdzenia cosinusów. Oznaczmy 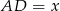AD = x . Mamy wtedy

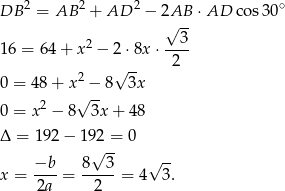
DB 2 = AB 2 + AD 2 − 2AB ⋅ AD cos30 ∘ √ -- 2 --3- 1 6 = 64 + x − 2 ⋅8x ⋅ 2 2 √ -- 0 = 48+ x√−--8 3x 0 = x2 − 8 3x + 48 Δ = 192 − 1 92 = 0 −b 8√ 3- √ -- x = ----= -----= 4 3. 2a 2

Pozostało teraz wyliczyć wysokość równoległoboku – liczymy ją z trójkąta prostokątnego 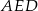AED .

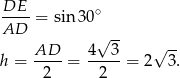
DE-- ∘ AD = sin3 0 √ -- √ -- h = AD-- = 4--3-= 2 3. 2 2

Zatem pole równoległoboku jest równe

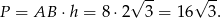
√ -- √ -- P = AB ⋅h = 8⋅ 2 3 = 16 3 .

Sposób II

Tym razem wyliczymy długość boku 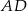AD korzystając z twierdzenia sinusów w trójkącie 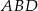ABD . Dokładniej, korzystając z twierdzenia sinusów, wyliczymy najpierw miarę kąta 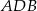ADB . Mamy

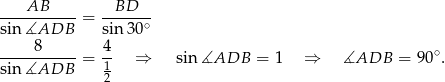
AB BD -----------= ------- sin ∡ADB sin 30∘ ----8------ 4- ∘ sin ∡ADB = 1 ⇒ sin ∡ADB = 1 ⇒ ∡ADB = 90 . 2

W takim razie trójkąt 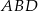ABD jest prostokątny i na mocy twierdzenia Pitagorasa mamy

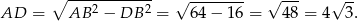
∘ ------------ √ -------- √ --- √ -- AD = AB 2 − DB 2 = 6 4− 16 = 48 = 4 3.

Wysokość i pole równoległoboku możemy teraz obliczyć jak w pierwszym sposobie, ale możemy też zrobić to odrobinę, szybciej korzystając ze wzoru na pole z sinusem.

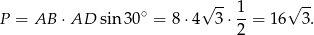
∘ √ -- 1 √ -- P = AB ⋅AD sin3 0 = 8 ⋅4 3 ⋅--= 1 6 3. 2

Sposób III

Zauważmy, że ponieważ 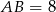AB = 8 i jednocześnie wiemy, że promień okręgu opisanego na trójkącie 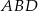ABD jest równy 4, więc 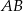AB jest średnicą tego okręgu. Zatem 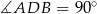∡ADB = 90∘ . Dalej liczymy jak w poprzednim sposobie.  
Odpowiedź: √ -- 16 3

Wersja PDF