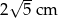Zadanie nr 4533514
W okrąg wpisano trapez równoramienny 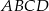 , którego podstawy mają długości:
, którego podstawy mają długości: 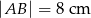 ,
, 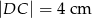 . Styczna do okręgu w punkcie
. Styczna do okręgu w punkcie 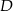 przecina prostą
przecina prostą 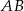 w punkcie
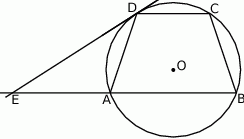
w punkcie 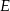 (rys). Wiedząc, że
(rys). Wiedząc, że 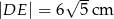 oblicz promień okręgu opisanego na trapezie
oblicz promień okręgu opisanego na trapezie  .
.
Rozwiązanie
Niech punkty 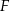 i
i 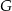 będą rzutami punktów
będą rzutami punktów 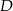 i
i 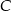 na podstawę
na podstawę 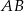 oraz niech
oraz niech 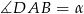 .
.
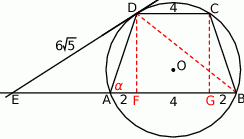
Korzystając z twierdzenia o siecznych mamy
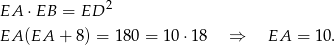
Jeżeli nie chcemy korzystać z twierdzenia o siecznych, to powinniśmy najpierw zauważyć, że trójkąty 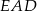 i
i 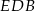 są podobne. Wtedy powyższy rachunek wynika z ich podobieństwa.
są podobne. Wtedy powyższy rachunek wynika z ich podobieństwa.
Obliczamy teraz długości: wysokości, ramienia i przekątnej trapezu.
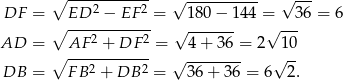
Promień okręgu opisanego na trapezie 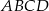 możemy teraz obliczyć korzystając z twierdzenia sinusów w trójkącie
możemy teraz obliczyć korzystając z twierdzenia sinusów w trójkącie 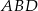 .
.
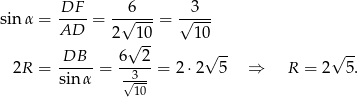
Odpowiedź: