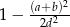Zadanie nr 4601113
Podstawy trapezu równoramiennego mają długości  i
i 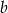 , a jego przekątna ma długość
, a jego przekątna ma długość 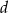 . Wyznacz cosinus kąta między przekątnymi tego trapezu.
. Wyznacz cosinus kąta między przekątnymi tego trapezu.
Rozwiązanie
Jak zwykle zaczynamy od rysunku.
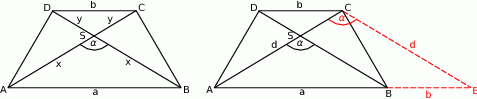
Sposób I
Jak wyliczyć szukany 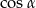 ? Najprościej byłoby zastosować twierdzenie cosinusów do trójkąta
? Najprościej byłoby zastosować twierdzenie cosinusów do trójkąta 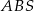 . Aby to zrobić musimy najpierw wyliczyć długość odcinka
. Aby to zrobić musimy najpierw wyliczyć długość odcinka 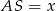 . Kluczowe do tego jest podobieństwo trójkątów
. Kluczowe do tego jest podobieństwo trójkątów 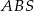 i
i 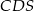 . Dzięki niemu, oraz dzięki równości
. Dzięki niemu, oraz dzięki równości 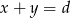 mamy
mamy
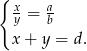
Mamy stąd
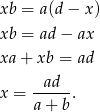
No i możemy napisać twierdzenie cosinusów dla trójkąta 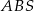 :
:
Sposób II
Tym razem bądźmy sprytniejsi i poprowadźmy przez punkt 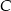 prostą równoległą do przekątnej
prostą równoległą do przekątnej 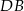 (prawy rysunek). Punkt wspólny tej prostej i podstawy
(prawy rysunek). Punkt wspólny tej prostej i podstawy 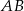 oznaczmy przez
oznaczmy przez 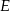 .
.
Zauważmy, że czworokąt 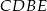 jest równoległobokiem, więc
jest równoległobokiem, więc 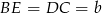 i
i 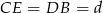 . Ponadto
. Ponadto 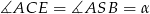 . Piszemy teraz twierdzenie cosinusów w trójkącie
. Piszemy teraz twierdzenie cosinusów w trójkącie 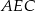 .
.
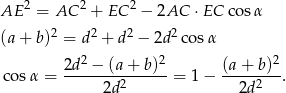
Odpowiedź: