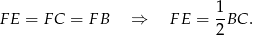Zadanie nr 4665263
Punkt 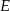 jest punktem wspólnym dwusiecznych kątów
jest punktem wspólnym dwusiecznych kątów 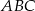 i
i 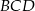 trapezu
trapezu 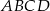 o podstawach
o podstawach 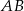 i
i 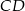 . Punkt
. Punkt 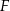 jest środkiem odcinka
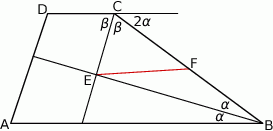
jest środkiem odcinka 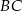 (zobacz rysunek).
(zobacz rysunek).
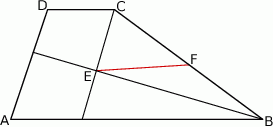
Wykaż, że 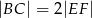 .
.
Rozwiązanie
Oznaczmy 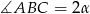 i
i 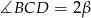 .
.
Zauważmy, że
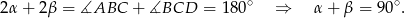
To oznacza, że trójkąt 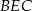 jest prostokątny. Teraz wystarczy zauważyć, że punkt
jest prostokątny. Teraz wystarczy zauważyć, że punkt 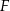 jest środkiem okręgu opisanego na trójkącie
jest środkiem okręgu opisanego na trójkącie 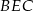 (bo okrąg o średnicy
(bo okrąg o średnicy 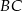 przechodzi przez punkt
przechodzi przez punkt 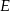 ). W takim razie
). W takim razie