/Szkoła średnia/Geometria/Planimetria/Czworokąt

Zadanie nr 4719510

Dodaj do ulubionych
Dodaj do rozwiązanych

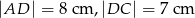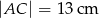W trapezie prostokątnym ABCD na rysunku poniżej dane są: |AD | = 8 cm ,|DC | = 7 cm oraz |AC | = 13 cm .

PIC

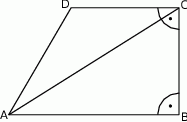
Oblicz:

  • miarę kąta ostrego trapezu przy wierzchołku A ,
  • długość odcinka łączącego środki ramion tego trapezu.

Rozwiązanie

  • Korzystając z twierdzenia cosinusów łatwo obliczyć cosinus kąta przy wierzchołku D . Liczymy
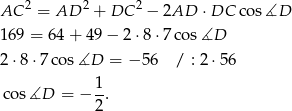
    2 2 2 AC = AD + DC − 2AD ⋅DC co s∡D 169 = 64 + 49 − 2 ⋅8 ⋅7co s∡D 2⋅8 ⋅7 cos∡D = − 56 / : 2⋅ 56 1 cos ∡D = − 2.

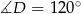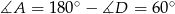    W takim razie ∘ ∡D = 120 i ∘ ∘ ∡A = 180 − ∡D = 60 .  
    Odpowiedź: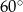 60∘

  • Dorysujmy wysokość DE trapezu.
    PIC

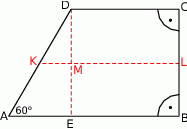
    Patrzymy na trójkąt prostokątny AED .

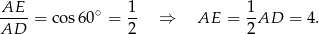
    AE--= cos 60∘ = 1- ⇒ AE = 1AD = 4. AD 2 2

    Sposób I

    Jak wiadomo odcinek KL łączący środki ramion trapezu ma długość równą średniej arytmetycznej długości podstaw trapezu. Zatem

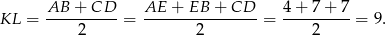
    AB-+--CD-- AE--+-EB-+--CD-- 4+--7+--7- KL = 2 = 2 = 2 = 9.

    Sposób II

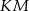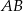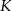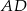    Zauważmy, że odcinek KM jest równoległy do prostej AB i przechodzi przez środek K boku AD trójkąta 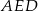AED . Jest to więc w tym trójkącie odcinek łączący środki boków. Zatem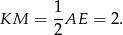

    1 KM = --AE = 2. 2

    Stąd

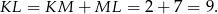
    KL = KM + ML = 2 + 7 = 9.

     
    Odpowiedź: 9 cm

Wersja PDF