/Szkoła średnia/Geometria/Planimetria/Czworokąt

Zadanie nr 4805390

Dodaj do ulubionych
Dodaj do rozwiązanych

Przekątne czworokąta 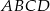ABCD są prostopadłe.

  • Wykaż, że sumy kwadratów przeciwległych boków tego czworokąta są równe.
  • Wykaż, że jeżeli długości jego boków 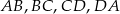AB ,BC ,CD ,DA są kolejnymi wyrazami ciągu geometrycznego to czworokąt ten jest rombem.

Rozwiązanie

Rozpocznijmy od szkicowego rysunku.

PIC

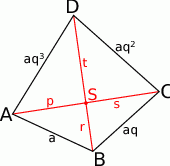
  • Jeżeli przez 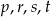p,r,s,t oznaczymy długości odcinków łączących wierzchołki czworokąta z punktem przecięcia się przekątnych to na mocy twierdzenia Pitagorasa mamy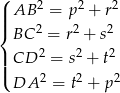
    ( | AB 2 = p2 + r2 ||{ 2 2 2 BC = r + s || CD 2 = s2 + t2 |( DA 2 = t2 + p2

    W takim razie

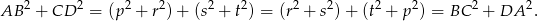
    AB 2 + CD 2 = (p2 + r2) + (s2 + t2) = (r2 + s2) + (t2 + p2) = BC 2 + DA 2.
  • Skoro długości boków są kolejnymi wyrazami ciągu geometrycznego, to możemy je oznaczyć przez 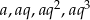2 3 a,aq ,aq ,aq . Na mocy poprzedniego podpunktu mamy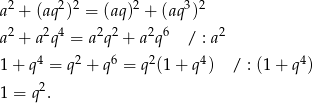
    a2 + (aq2)2 = (aq)2 + (aq3)2 2 2 4 2 2 2 6 2 a + a q = a q + a q / : a 1 + q4 = q2 + q6 = q 2(1 + q4) / : (1 + q4) 2 1 = q .

    Oczywiście 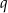q nie może być ujemne, czyli 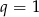q = 1 i wszystkie boki czworokąta mają równe długości.

Wersja PDF