Zadanie nr 4883249
Na okręgu o promieniu 5 opisano deltoid o obwodzie 60. Oblicz pole deltoidu.
Rozwiązanie
Jak to często bywa w zadaniach z geometrii, najważniejszy jest rysunek.
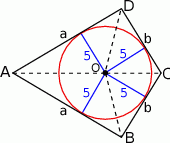
Jeżeli połączymy środek okręgu wpisanego w czworokąt z jego wierzchołkami, to otrzymamy cztery trójkąty 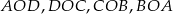 , które w sumie dają cały deltoid. Zatem wystarczy obliczyć sumę ich pól. To nie jest jednak trudne, bo wysokością każdego z nich jest promień okręgu wpisanego. Zatem
, które w sumie dają cały deltoid. Zatem wystarczy obliczyć sumę ich pól. To nie jest jednak trudne, bo wysokością każdego z nich jest promień okręgu wpisanego. Zatem
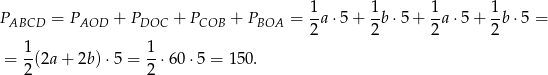
Po drodze skorzystaliśmy z podanego obwodu czworokąta.
Dwie uwagi. Po pierwsze wyprowadziliśmy wzór na pole czworokąta opisanego na okręgu
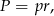
gdzie 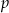 jest połową obwodu, a
jest połową obwodu, a  jest promieniem okręgu wpisanego. Jeżeli znamy ten wzór, to oczywiście mogliśmy od razu z niego skorzystać.
jest promieniem okręgu wpisanego. Jeżeli znamy ten wzór, to oczywiście mogliśmy od razu z niego skorzystać.
Druga uwaga: w rozwiązaniu nie było ważne, że czworokąt jest deltoidem.
Odpowiedź: 150

