Zadanie nr 4890981
W czworokącie wypukłym 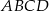 dane są:
dane są: 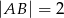 ,
, 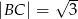 ,
, 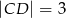 ,
, 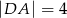 i
i 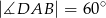 . Oblicz pole tego czworokąta.
. Oblicz pole tego czworokąta.
Rozwiązanie
Jak zwykle, zacznijmy od schematycznego rysunku.
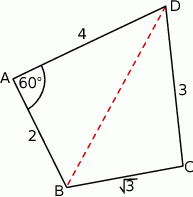
Plan rozwiązania zadania jest następujący. Aby obliczyć pole czworokąta, podzielimy go na dwa trójkąty (przekątną 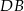 ). Pole każdego z nich obliczymy ze wzoru
). Pole każdego z nich obliczymy ze wzoru
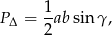
gdzie 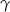 – kąt między bokami
– kąt między bokami  i
i 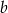 . Jedyna rzecz, której nam brakuje, to miara kąta przy wierzchołku
. Jedyna rzecz, której nam brakuje, to miara kąta przy wierzchołku 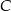 . Będziemy mogli go wyliczyć z twierdzenia kosinusów, jeżeli będziemy znali długość
. Będziemy mogli go wyliczyć z twierdzenia kosinusów, jeżeli będziemy znali długość 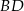 , a tę możemy wyliczyć znowu z twierdzenia kosinusów, ale w trójkącie
, a tę możemy wyliczyć znowu z twierdzenia kosinusów, ale w trójkącie 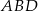 .
.
No dobrze, skoro wszystko już wiemy, to do dzieła. Liczymy 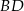 :
:
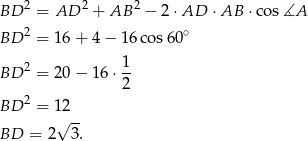
Liczymy teraz 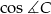 :
:
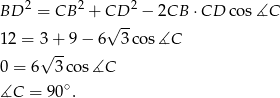
Jak już wiemy co wyszło, to wiemy, że można było to wyliczyć z twierdzenia Pitagorasa, ale to przegapiliśmy, trudno. Teraz bez trudu liczymy szukane pola
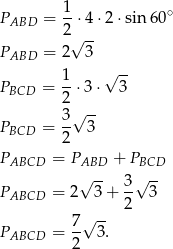
Odpowiedź: