/Szkoła średnia/Geometria/Planimetria/Czworokąt

Zadanie nr 5016465

Dodaj do ulubionych
Dodaj do rozwiązanych

W trapez równoramienny o obwodzie 20 i przekątnej długości 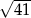√ --- 41 można wpisać okrąg. Oblicz odległości punktu przecięcia przekątnych tego trapezu od prostych zawierających jego boki.

Rozwiązanie

Zacznijmy od rysunku i oznaczmy krótszą podstawę trapezu przez a , ramię przez c a wysokość przez h .

PIC

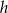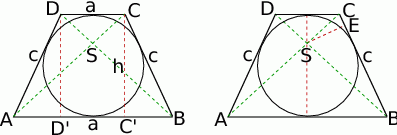
Ponieważ w trapez można wpisać okrąg, sumy długości przeciwległych boków są równe. Ponieważ obwód jest równy 20, to sumy te są równe po 10. W szczególności

c = 5.

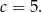
Na rysunku widzimy jak wysokości trapezu dzielą dłuższą podstawę na trzy odcinki, środkowy ma długość a , a dwa pozostałe będą mieć długość 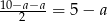10−a−a- 2 = 5 − a . W takim razie 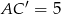′ AC = 5 . Liczymy teraz wysokość 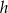h z trójkąta prostokątnego ′ AC C .

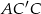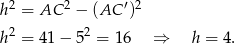
2 2 ′2 h = AC − (AC ) h2 = 41 − 52 = 16 ⇒ h = 4 .

Mając wysokość, łatwo wyliczyć długości podstaw trapezu.

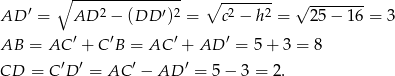
--------------- ′ ∘ 2 ′ 2 ∘ -2----2 √ -------- AD = AD − (DD ) = c − h = 25 − 1 6 = 3 AB = AC ′ + C ′B = AC ′ + AD ′ = 5+ 3 = 8 CD = C′D ′ = AC ′ − AD ′ = 5 − 3 = 2.

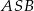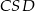Ponieważ trójkąty ASB i CSD są podobne, stosunek ich wysokości opuszczonych z wierzchołka 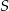S jest równy stosunkowi ich podstaw i wynosi

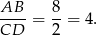
AB 8 ---- = --= 4. CD 2

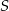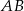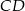Zatem odległości punktu S od podstaw AB i CD są równe odpowiednio

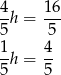
4 16 5h = 5-- 1h = 4- 5 5

Aby obliczyć odległość punktu 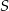S od ramion trapezu zauważmy, że

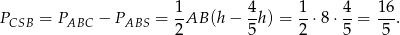
1 4 1 4 16 PCSB = PABC − PABS = -AB (h − -h) = --⋅8 ⋅--= ---. 2 5 2 5 5

Zatem ze wzoru na pole mamy

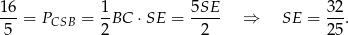
16 1 5SE 32 ---= PCSB = -BC ⋅SE = ---- ⇒ SE = --. 5 2 2 25

 
Odpowiedź: Od podstaw: 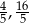4 16 5, 5 , od ramion: 3225

Wersja PDF