/Szkoła średnia/Geometria/Planimetria/Czworokąt

Zadanie nr 5077874

Dodaj do ulubionych
Dodaj do rozwiązanych

W czworokącie wypukłym 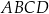ABCD , długości boków 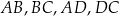AB ,BC ,AD ,DC są kolejnymi wyrazami ciągu arytmetycznego. Wykaż, że dwusieczne kątów wewnętrznych tego czworokąta przecinają się w jednym punkcie.

Rozwiązanie

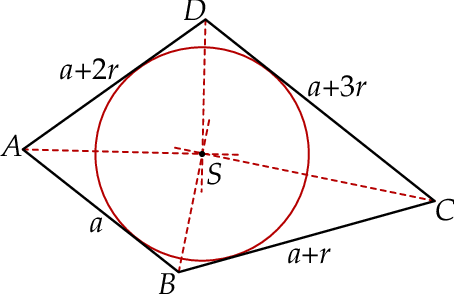
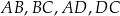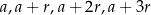Jeżeli długości boków AB ,BC ,AD ,DC są kolejnymi wyrazami ciągu arytmetycznego, to możemy te długości oznaczyć przez a,a+ r,a + 2r,a + 3r .

ZINFO-FIGURE

W szczególności,

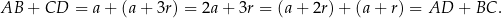
AB + CD = a + (a + 3r) = 2a + 3r = (a+ 2r )+ (a + r) = AD + BC .

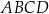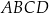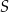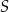To oznacza, że w czworokąt ABCD można wpisać okrąg. Środkiem tego okręgu jest punkt, który leży na każdej z dwusiecznych czworokąta ABCD (bo odległość punktu S od każdego boku jest taka sama). Dwusieczne te przecinają się więc w punkcie S .

Wersja PDF