Zadanie nr 5109257
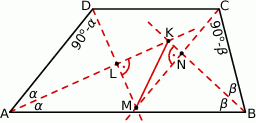
Dwusieczne kątów wewnętrznych trapezu 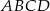 przecinają się w punktach
przecinają się w punktach 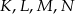 (patrz rysunek). Wykaż, że
(patrz rysunek). Wykaż, że 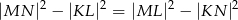 .
.
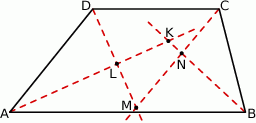
Rozwiązanie
Jeżeli oznaczymy 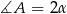 i
i 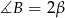 , to mamy
, to mamy
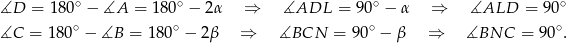
To oznacza, ż trójkąty 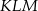 i
i  są prostokątne.
są prostokątne.
Na mocy twierdzenia Pitagorasa mamy więc
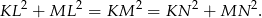
A to jest dokładnie równość, którą mieliśmy udowodnić.

