Zadanie nr 5165523
Punkty 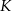 i
i 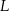 dzielą podstawę
dzielą podstawę 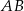 trapezu
trapezu 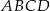 na trzy równe części, a punkty
na trzy równe części, a punkty 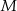 i
i 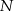 dzielą podstawę
dzielą podstawę 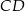 tego trapezu na trzy równe części. Pole czworokąta
tego trapezu na trzy równe części. Pole czworokąta 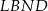 jest równe
jest równe 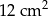 . Oblicz pole trapezu
. Oblicz pole trapezu 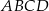 .
.
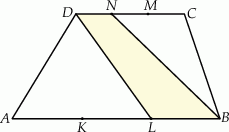
Rozwiązanie
Jeżeli oznaczymy długości podstaw trapezu 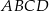 przez
przez 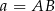 i
i 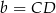 , a przez
, a przez 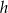 jego wysokość, to czworokąt
jego wysokość, to czworokąt 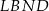 jest trapezem o podstawach długości
jest trapezem o podstawach długości 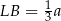 ,
, 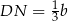 i wysokości
i wysokości 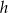 . Mamy zatem
. Mamy zatem
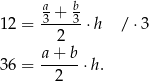
To oznacza, że pole trapezu 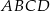 jest równe
jest równe 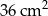 .
.
Odpowiedź: