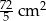Zadanie nr 5179452
Środek okręgu wpisanego w trapez prostokątny znajduje się w odległości 2 cm i 4 cm od końców ramienia pochyłego danego trapezu. Znaleźć pole trapezu.
Rozwiązanie
Naszkicujmy sobie opisaną sytuację.
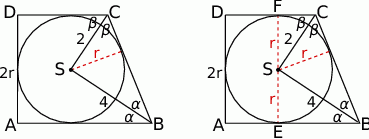
Sposób I
Po pierwsze zauważmy, że
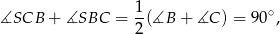
co oznacza, że trójkąt 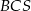 jest prostokątny. W dodatku, jego wysokość opuszczona z wierzchołka
jest prostokątny. W dodatku, jego wysokość opuszczona z wierzchołka  jest równa promieniowi okręgu wpisanego w trapez. Porównując dwa wzory na pole trójkąta
jest równa promieniowi okręgu wpisanego w trapez. Porównując dwa wzory na pole trójkąta 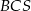 mamy
mamy
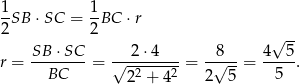
W czworokącie opisanym na okręgu sumy przeciwległych boków są równe, zatem
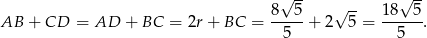
Możemy więc wyliczyć pole.
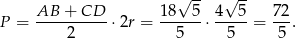
Sposób II
Tak jak w poprzednim sposobie zauważamy, że 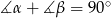 . Z trójkątów prostokątnych
. Z trójkątów prostokątnych 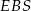 i
i 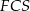 mamy
mamy
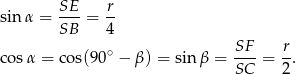
Podstawiamy te wartości do jedynki trygonometrycznej i mamy
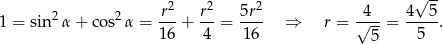
Teraz raz jeszcze patrzymy na trójkąty prostokątne  i
i  .
.
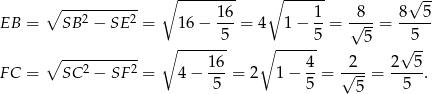
Pole trapezu jest więc równe
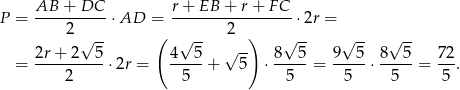
Odpowiedź: