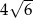/Szkoła średnia/Geometria/Planimetria/Czworokąt

Zadanie nr 5187684

Dodaj do ulubionych
Dodaj do rozwiązanych

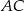Dany jest prostokąt ABCD . Z wierzchołków B i D poprowadzono proste prostopadłe do przekątnej AC dzielące ją na trzy odcinki 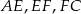AE ,EF ,F C , każdy długości 4. Oblicz długość boków prostokąta.

Rozwiązanie

Zaczynamy od rysunku

PIC

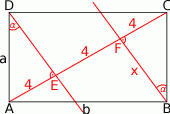
Po pierwsze zauważmy, że

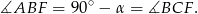
∡ABF = 90∘ − α = ∡BCF .

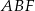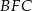Zatem trójkąty ABF i BF C mają dwa takie same kąty, więc muszą być podobne. Stąd

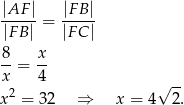
|AF--|= |FB-| |F B| |FC | 8 x --= -- x 4 √ -- x 2 = 32 ⇒ x = 4 2.

Teraz z twierdzenia Pitagorasa możemy obliczyć długości boków prostokąta

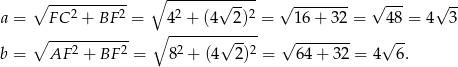
∘ ------------- ∘ ---2------2 2 √ --2 √ -------- √ --- √ -- a = F C + BF = ∘ 4--+-(4---2)-= 16 + 32 = 4 8 = 4 3 ∘ ----------- √ -- √ -------- √ -- b = AF 2 + BF 2 = 82 + (4 2)2 = 64 + 32 = 4 6.

 
Odpowiedź: 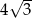√ -- 4 3 i √ -- 4 6

Wersja PDF