Zadanie nr 5191821
Na bokach 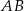 i
i 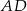 rombu
rombu 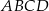 wybrano odpowiednio punkty
wybrano odpowiednio punkty 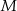 i
i 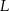 w ten sposób, że
w ten sposób, że 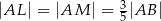 . Odcinek
. Odcinek 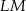 jest styczny do okręgu wpisanego w romb
jest styczny do okręgu wpisanego w romb 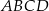 . Punkt
. Punkt 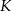 jest punktem styczności okręgu wpisanego w ten romb z bokiem
jest punktem styczności okręgu wpisanego w ten romb z bokiem 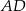 (zobacz rysunek).
(zobacz rysunek).
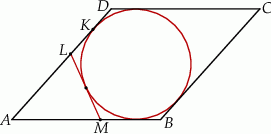
Wykaż, że 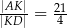 .
.
Rozwiązanie
Dorysujmy przekątne rombu oraz połączmy środek 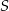 okręgu wpisanego w romb z punktem
okręgu wpisanego w romb z punktem 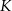 .
.
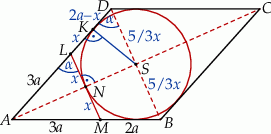
Wiemy, że
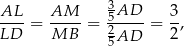
więc możemy oznaczyć 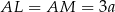 i
i 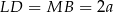 .
.
Przekątna 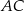 jest osią symetrii danego rysunku, więc przecina odcinek
jest osią symetrii danego rysunku, więc przecina odcinek 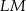 w jego środku – oznaczmy ten punkt przez
w jego środku – oznaczmy ten punkt przez 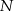 . Jeżeli oznaczymy
. Jeżeli oznaczymy 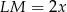 , to
, to
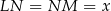
oraz
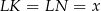
(odcinki stycznych do okręgu). Trójkąty 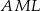 i
i 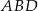 są podobne, więc
są podobne, więc
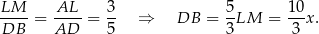
Stąd
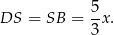
Popatrzmy teraz na trójkąty prostokątne 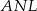 i
i 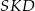 . Mamy w nich
. Mamy w nich
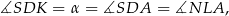
więc są podobne. Stąd
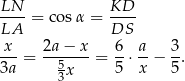
Jeżeli oznaczmy 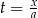 , to mamy
, to mamy
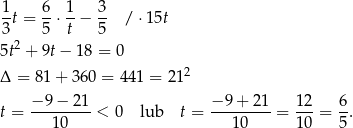
To oznacza, że