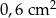/Szkoła średnia/Geometria/Planimetria/Czworokąt

Zadanie nr 5432624

Dodaj do ulubionych
Dodaj do rozwiązanych

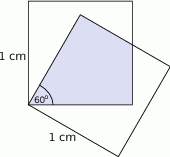
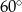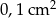Kwadratowe szklane płytki o boku długości 1 cm, połączone w jednym wierzchołku, rozsunęły się tak, że boki wychodzące z jednego wierzchołka tworzą ze sobą kąt 60∘ . Oblicz pole części wspólnej płytek. Wynik podaj z dokładnością do 0,1 cm 2 .

PIC

Rozwiązanie

Sposób I

Jeżeli dorysujemy odcinek 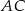AC jak na obrazku, to otrzymamy dwa przystające trójkąty prostokątne.

PIC

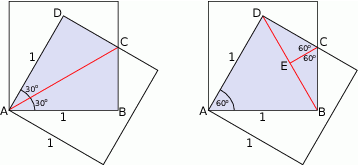
Jedna z przyprostokątnych tych trójkątów ma długość 1, spróbujmy wyliczyć długość drugiej. Mamy

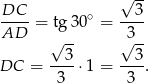
DC √ 3- ---- = tg3 0∘ = ---- AD √ -- √3-- 3 3 DC = ---⋅ 1 = ----. 3 3

Zatem pole jednego trójkąta wynosi

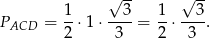
√ -- √ -- PACD = 1-⋅1 ⋅--3-= 1-⋅--3-. 2 3 2 3

Zatem

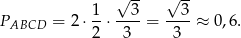
√ -- √ -- PABCD = 2 ⋅ 1-⋅-3-= --3-≈ 0,6. 2 3 3

Sposób II

Tym razem dorysujmy odcinek 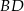BD . Trójkąt 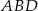ABD jest równoramienny i kąt między ramionami jest równy 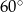∘ 60 , zatem pozostałe kąty też muszą być równe 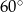60 ∘ i trójkąt ten jest równoboczny. Jego pole jest równe

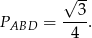
√ -- P = --3-. ABD 4

Pozostało policzyć pole trójkąta 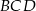BCD . Ponieważ suma kątów w czworokącie 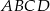ABCD jest równa 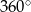360∘ , mamy

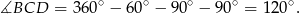
∡BCD = 3 60∘ − 60∘ − 90∘ − 90∘ = 1 20∘.

Trójkąt 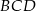BCD możemy więc podzielić na dwa trójkąty prostokątne o kącie ostrym 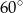60∘ . Mamy więc

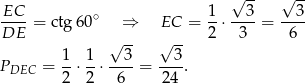
√ -- √ -- EC-- ∘ 1- --3- ---3 DE = ctg6 0 ⇒ EC = 2 ⋅ 3 = 6 √ -- √ -- PDEC = 1⋅ 1-⋅--3-= --3. 2 2 6 24

Zatem pole czworokąta ABCD jest równe

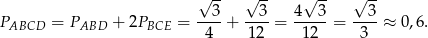
√ -- √ -- √ -- √ -- P = P + 2P = --3-+ --3-= 4--3-= --3-≈ 0,6. ABCD ABD BCE 4 12 12 3

 
Odpowiedź: 2 0,6 cm

Wersja PDF