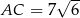Zadanie nr 5558424
Czworokąt 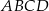 jest wpisany w okrąg o promieniu
jest wpisany w okrąg o promieniu 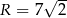 . Kąt
. Kąt 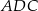 tego czworokąta jest ostry i jego miara jest o
tego czworokąta jest ostry i jego miara jest o 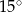 większa od miary kąta
większa od miary kąta 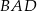 . Iloczyn sinusów wszystkich kątów wewnętrznych czworokąta
. Iloczyn sinusów wszystkich kątów wewnętrznych czworokąta 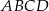 jest równy
jest równy  . Oblicz długości przekątnych
. Oblicz długości przekątnych 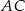 i
i 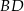 tego czworokąta.
tego czworokąta.
Rozwiązanie
Szkicujemy opisaną sytuację.
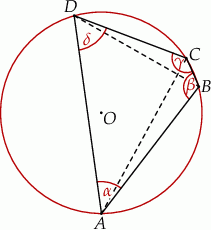
Jeżeli oznaczmy miary kątów wewnętrznych czworokąta 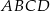 tak jak na powyższym rysunku, to mamy
tak jak na powyższym rysunku, to mamy
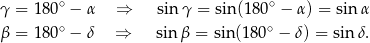
Informacje podane w treści zadania możemy więc zapisać w postaci
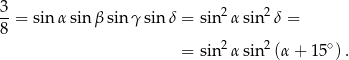
Sinusy kątów wypukłych są nieujemne, więc mamy stąd
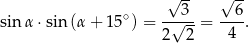
Możemy otrzymaną zależność przekształcić na różne sposoby, ale najpierw obliczmy funkcje trygonometryczne kąta 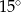 .
.
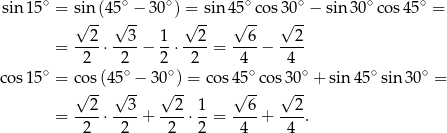
Sposób I
Korzystamy ze wzoru na sinus sumy.
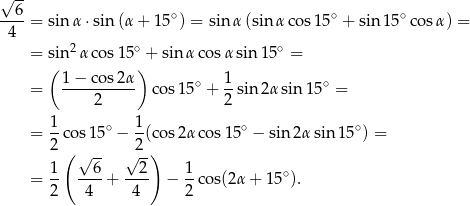
Stąd
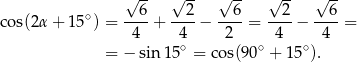
Ponieważ  jest kątem ostrym oznacza to, że
jest kątem ostrym oznacza to, że
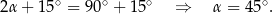
To w połączeniu z twierdzeniem sinusów pozwala obliczyć długość przekątnej 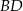
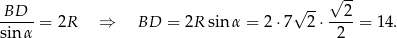
Podobnie obliczmy długość drugiej przekątnej.
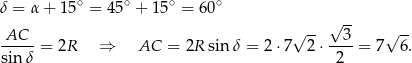
Sposób II
Tym razem będziemy chcieli skorzystać ze wzoru na różnicę sinusów
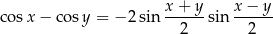
Prawa strona tego wzoru bardzo przypomina lewą stronę otrzymanej przez nas równości
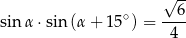
Odpowiednie wartości  i
i 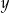 możemy wyznaczyć z warunku
możemy wyznaczyć z warunku
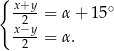
Po dodaniu tych równań stronami mamy 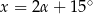 , a po odjęciu
, a po odjęciu 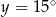 . Mamy zatem
. Mamy zatem
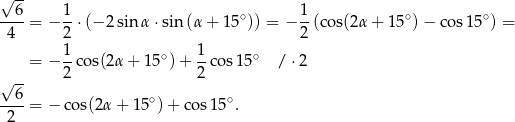
Korzystamy teraz z wcześniej obliczonych wartości 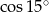 i
i 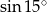 .
.
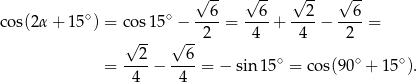
Ponieważ  jest kątem ostrym, mamy stąd
jest kątem ostrym, mamy stąd
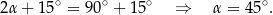
Długości przekątnych obliczamy tak samo jak w pierwszym sposobie.
Odpowiedź: 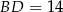 ,
,