/Szkoła średnia/Geometria/Planimetria/Czworokąt

Zadanie nr 5635223

Dodaj do ulubionych
Dodaj do rozwiązanych

Obwód równoległoboku 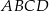ABCD jest równy 26, miara jego kąta rozwartego 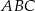ABC jest równa 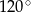120∘ , a promień okręgu wpisanego w trójkąt 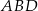ABD jest równy 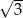√ -- 3 . Oblicz długości boków równoległoboku ABCD .

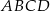Rozwiązanie

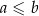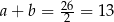Oznaczmy boki równoległoboku przez a ≤ b . Wiemy wtedy, że 26 a + b = 2 = 13 .

PIC

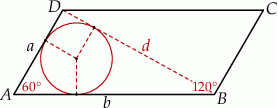
Musimy jakość wykorzystać podaną informację o promieniu okręgu wpisanego w trójkąt 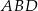ABD . Jest w zasadzie tylko jeden sposób, żeby to zrobić – wzór na pole trójkąta: 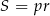S = pr , gdzie 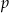p jest połową jego obwodu. Żeby móc z niego skorzystać, obliczmy najpierw długość 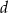d przekątnej 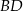BD . Piszemy twierdzenie cosinusów w trójkącie ABD .

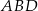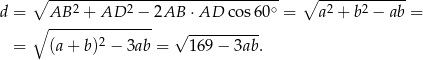
∘ ----2------2-------------------∘ ∘ -2----2----- d = AB---+--AD---−-2AB ⋅AD cos 60 = a + b − ab = ∘ 2 √ ---------- = (a + b) − 3ab = 169 − 3ab.

Porównujemy teraz dwa wzory na pole trójkąta 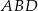ABD .

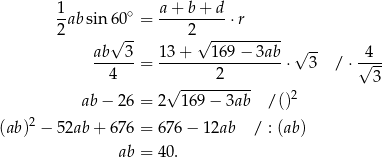
1ab sin 60∘ = a+--b+-d-⋅r 2 2 ab√ 3- 13+ √ 169-−-3ab- √ -- 4 ------= -----------------⋅ 3 / ⋅√--- 4 √ ----2----- 3 ab − 26 = 2 169− 3ab / ()2 (ab)2 − 52ab+ 676 = 6 76− 12ab / : (ab) ab = 4 0.

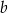Na mocy wzorów Viéte‘a to oznacza, że liczby a i b są pierwiastkami równania kwadratowego

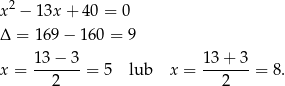
2 x − 13x + 40 = 0 Δ = 169 − 16 0 = 9 13 − 3 13 + 3 x = -------= 5 lub x = -------= 8. 2 2

 
Odpowiedź: 5 i 8

Wersja PDF